Trong mặt phẳng Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có H
là chân đường cao hạ từ A lên BD. Trung điểm BC là M(-1;0). . Phương trình đường trung tuyến kẻ từ A của tam giác ADH là 7x+y-3=0. Tọa độ đỉnh D(a;b). Tính a+b
Trong mặt phẳng Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có H\(\left(\frac{-6}{5};\frac{7}{5}\right)\) là chân đường cao hạ từ A lên BD. Trung điểm BC là M(-1;0). . Phương trình đường trung tuyến kẻ từ A của tam giác ADH là 7x+y-3=0. Tọa độ đỉnh D(a;b). Tính a+b
Gọi P là trung điểm AH, Q là trung điểm DH \(\Rightarrow\) PQ là đường trung bình tam giác ADH \(\Rightarrow\left\{{}\begin{matrix}PQ//AD\\PQ=\frac{1}{2}AD\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}PQ//BM\\PQ=BM\end{matrix}\right.\)
\(\Rightarrow PQMB\) là hbh \(\Rightarrow BP//MQ\)
Mặt khác \(PQ//AD\Rightarrow PQ\perp AB\Rightarrow\) P là trực tâm tam giác ABQ
\(\Rightarrow BP\perp AQ\Rightarrow MQ\perp AQ\) (với AQ là trung tuyến kẻ từ A của ADH)
\(\Rightarrow\) Đường thẳng MQ nhận \(\left(1;-7\right)\) là 1 vtpt
Phương trình MQ: \(1\left(x+1\right)-7y=0\Leftrightarrow x-7y+1=0\)
Q là giao AQ và MQ nên tọa độ thỏa mãn: \(\left\{{}\begin{matrix}x-7y+1=0\\7x+y-3=0\end{matrix}\right.\) \(\Rightarrow Q\left(\frac{2}{5};\frac{1}{5}\right)\)
Q là trung điểm DH \(\Rightarrow D\left(2;-1\right)\)
Trong mặt phẳng hệ tọa độ Oxy , cho hình chữ nhật ABCD tâm O. Biết phương trình đường thẳng AB:x--y+5=0 và trung điểm M của cạnh BC thuộc đường thẳng x+3y-6=0, xác định tọa độ các đỉnh của hình chữ nhật ABCD
Phương trình đường thẳng qua O và song song AB có dạng:
Tọa độ M là nghiệm của hệ:
Phương trình đường thẳng BC qua M, nhận là 1 vtpt có dạng:
Tọa độ B là nghiệm của hệ:
M là trung điểm BC tọa độ C
O là trung điểm AC tọa độ A
O là trung điểm BD
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có hình chiếu vuông góc của A lên đường thẳng BD là H(-1/5;2/5), điểm M(0;-1) là trung điểm cạnh BC và điểm N(7/5;-4/5) là trung điểm của đoạn HD. Tìm tọa độ các đỉnh của hình chữ nhật ABCD.
a) Trong mặt phẳng Oxy, cho hình chữ nhật ABCD có đỉnh A(3;5), đường thẳng BC:x+y-2=0. Biết điểm E(6;0) thuộc cạnh CD. Tính diện tích hình chữ nhật ABCD.
b) Trong mặt phẳng Oxy, tìm tọa độ điểm M thuộc đường thẳng d:{x=1+t và y=2-3t sao cho khoảng cách từ điểm M đến đường thẳng đenta: 3x+4y+5=0 bằng 4.
a/ CD qua E và vuông góc BC nên pt có dạng:
\(1\left(x-6\right)-1\left(y-0\right)=0\Leftrightarrow x-y-6=0\)
Ta có: \(AB=d\left(A;BC\right)=\frac{\left|3+5-2\right|}{\sqrt{1^2+1^2}}=3\sqrt{2}\)
\(AD=d\left(A;CD\right)=\frac{\left|3-5-6\right|}{\sqrt{1^2+\left(-1\right)^2}}=4\sqrt{2}\)
\(\Rightarrow S_{ABCD}=AB.AD=24\)
b/ Do M thuộc d nên tọa độ có dạng: \(M\left(1+t;2-3t\right)\)
Áp dụng công thức khoảng cách:
\(d\left(M;\Delta\right)=4\Leftrightarrow\frac{\left|3\left(1+t\right)+4\left(2-3t\right)+5\right|}{\sqrt{3^2+4^2}}=4\)
\(\Leftrightarrow\left|16-9t\right|=20\Rightarrow\left[{}\begin{matrix}16-9t=20\\16-9t=-20\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}t=-\frac{4}{9}\\t=4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}M\left(\frac{5}{9};\frac{10}{3}\right)\\M\left(5;-10\right)\end{matrix}\right.\)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, mặt bên SAD là tam giác đều cạnh 2a và nằm trong mặt phẳng vuông góp với mặt phẳng (ABCD). Góc giữa mặt phẳng (SBC) và mặt phẳng (ABCD) là 30 0 . Thể tích của khối chóp S.ABCD là:
A. 2 a 3 3 3
B. a 3 3 3
C. 4 a 3 3 3
D. 2 a 3 3
Trong mặt phẳng Oxy cho HCN ABCD có điểm B (1;3) và diện tích là 30goij E là điểm nằm trên cạnh BC sao cho EC =2EB điểm H(5/2;5/2) là hình chiếu vuông góc trên DE Biết C có tung độ âm , Tìm tọa độ các hình chữ nhật
trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD có đỉnh A(-1,2) và tâm I(1/2:0) xác định tọa độ các đỉnh còn lại của hình chữ nhật ABCD, biết đường thẳng BC đi qua điểm m(4;-3)
I là trung điểm AC \(\Rightarrow C\left(2;-2\right)\)
\(\Rightarrow\overrightarrow{CM}=\left(2;-1\right)\Rightarrow\) đường thẳng BC có dạng:
\(1\left(x-2\right)+2\left(y+2\right)=0\Leftrightarrow x+2y+2=0\)
Đường thẳng AB qua A và vuông góc BC nên nhận \(\left(2;-1\right)\) là 1 vtpt
Phương trình AB:
\(2\left(x+1\right)-1\left(y-2\right)=0\Leftrightarrow2x-y+4=0\)
B là giao điểm AB và BC nên tọa độ là nghiệm:
\(\left\{{}\begin{matrix}x+2y+2=0\\2x-y+4=0\end{matrix}\right.\) \(\Rightarrow B\left(...\right)\)
I là trung điểm BD \(\Rightarrow\left\{{}\begin{matrix}x_D=2x_I-x_B=...\\y_D=2y_I-y_B=...\end{matrix}\right.\)
Trong mặt phẳng Oxy, cho elip (E) có tâm sai e bằng 2 2 và cắt đường tròn (C) có phương trình x 2 + y 2 = 5 tại bốn điểm tạo thành hình chữ nhật ABCD có AB=2AD. Phương trình chính tắc của (E) là
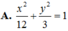
![]()
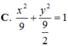
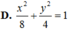
Trên mặt phẳng Oxy, hình chữ nhật ABCD có đỉnh A(3;- 1) và là hai trong bốn đường thẳng chứa bốn cạnh của hình chữ nhật đó. Diện tích của ABCD bằng
Thay tọa độ A vào 2 pt đường thẳng không thỏa mãn, vậy đó là 2 pt đường thẳng của các cạnh BC và CD
\(\Rightarrow\) Khoảng cách từ A đến 2 đường thẳng nói trên bằng độ dài 2 cạnh của hcn
\(\Rightarrow S=d\left(A;\Delta_1\right).d\left(A;\Delta_2\right)=\dfrac{\left|3-2.\left(-1\right)+1\right|}{\sqrt{1^2+\left(-2\right)^2}}.\dfrac{\left|2.3-1\right|}{\sqrt{2^2+1^2}}=6\)
Trong mặt phẳng với hệ tọa độ Oxy, cho hình chữ nhật ABCD. Gọi H là hình chiếu của A lên BD; I là trung điểm của BH. Biết đỉnh A(2;1), phương trình đường chéo BD là: x + 5y - 19 = 0, điểm I\(\left(\dfrac{42}{13};\dfrac{41}{13}\right)\). Tìm phương trình tổng quát của đường thẳng AD.