a : a/4 ( a khác o )

Những câu hỏi liên quan
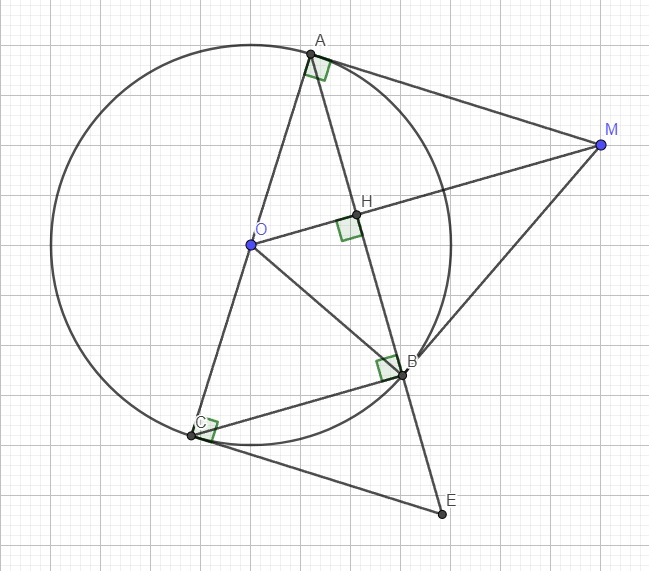
Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)a, Chứng minh 4 điểm A,B,O,C thuộc một đường trònb. Trên cung nhỏ BC của (O) lấy điểm M ( M khác B, M khác C, M khác AO). Tiếp tuyến tại M cắt AB,AC lần lượt tại D và E. Chứng minh chu vi tam giác ADE2ABc, Đường thẳng vuông góc với AO tại O cắt AB và AC lần lượt tại P và Q. Chứng minh 4PO.QEPQ² Các a/chị ơi, e đang thắc mắc ở câu c ạ, hai câu a và b thì e đã có cách làm rồi ạ. Cảm ơn a/chị thậ...
Đọc tiếp
 Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)
Cho điểm A nằm ngoài đường tròn (O), kẻ các tiếp tuyến AB,AC với đường tròn (O) (B,C là các tiếp điểm)
a, Chứng minh 4 điểm A,B,O,C thuộc một đường tròn
b. Trên cung nhỏ BC của (O) lấy điểm M ( M khác B, M khác C, M khác AO). Tiếp tuyến tại M cắt AB,AC lần lượt tại D và E. Chứng minh chu vi tam giác ADE=2AB
c, Đường thẳng vuông góc với AO tại O cắt AB và AC lần lượt tại P và Q. Chứng minh 4PO.QE=PQ²
Các a/chị ơi, e đang thắc mắc ở câu c ạ, hai câu a và b thì e đã có cách làm rồi ạ. Cảm ơn a/chị thật nhiều ạ
a: Xét tứ giác ABOC có
\(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
=>ABOC là tứ giác nội tiếp
=>A,B,O,C cùng thuộc một đường tròn
b: Xét (O) có
DB,DM là các tiếp tuyến
Do đó: DB=DM
Xét (O) có
EM,EC là các tiếp tuyến
Do đó: EM=EC
Chu vi tam giác ADE là:
\(C_{ADE}=AD+DE+AE\)
\(=AD+DM+ME+AE\)
\(=AD+DB+CE+AE\)
\(=AB+AC=2\cdot AB\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A). a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).c) Gọi H là giao điểm của AC và OE. Chứng minh AB^24OH.OE
Đọc tiếp
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A). a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).c) Gọi H là giao điểm của AC và OE. Chứng minh \(AB^2=4OH.OE\)
a: Xét tứ giác AECO có
\(\widehat{EAO}+\widehat{ECO}=90^0+90^0=180^0\)
=>AECO là tứ giác nội tiếp
=>A,E,C,O cùng thuộc một đường tròn
b: Ta có: ΔOBC cân tại O
mà OF là đường trung tuyến
nên OF là tia phân giác của góc COB
Xét ΔCOF và ΔBOF có
OC=OB
\(\widehat{COF}=\widehat{BOF}\)
OF chung
Do đó: ΔOCF=ΔOBF
=>\(\widehat{OCF}=\widehat{OBF}\)
mà \(\widehat{OCF}=90^0\)
nên \(\widehat{OBF}=90^0\)
=>FB là tiếp tuyến của (O)
c: Xét (O) có
EA,EC là các tiếp tuyến
=>EA=EC
=>E nằm trên đường trung trực của AC(1)
Ta có: OA=OC
=>O nằm trên đường trung trực của AC(2)
Từ (1) và (2) suy ra OE là đường trung trực của AC
=>OE\(\perp\)AC tại H và H là trung điểm của AC
Xét ΔAEO vuông tại A có AH là đường cao
nên \(OH\cdot OE=OA^2\)
=>\(4\cdot OH\cdot OE=4\cdot OA^2=\left(2\cdot OA\right)^2=AB^2\)
Đúng 1
Bình luận (0)
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A).
a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.
b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).
c) Gọi H là giao điểm của AC và OE. Chứng minh AB^24OH.OE
Đọc tiếp
Cho đường tròn (O; R) đường kính AB. Vẽ tiếp tuyến Ax với đường tròn (O). Trên tia Ax lấy điểm E khác A. Vẽ tiếp tuyến EC với đường tròn (O) (E là tiếp điểm, C khác A).
a) CM: 4 điểm A, E, C, O cùng thuộc một đường tròn.
b) Gọi K là trung điểm của BC. Tia OK cắt tia EC tại F. Chứng minh BF là tiếp tuyến của đường tròn (O).
c) Gọi H là giao điểm của AC và OE. Chứng minh \(AB^2=4OH.OE\)
Biết a/a' = b/b' = c/c' = 4 và a' + b' + c' khác 0 , a' = 3b' + 2c' khác o
Tính :
a ) a+b+c/a'+b'+c'
b ) a-3b+2c/a'-3b'+2c'
Từ bốn chữ số a,b,c,d khác nhau và khác o, ta lập số tự nhiên lớn nhất có 4 chữ số khác và số tự nhiên nhỏ nhất có 4 chữ số khác nhau. Tổng của hai số này bằng 15664. Tổng a+b+c+d là
abcd + dcba = 15664
1000*a+100*b+10*c+d+1000*d+100*c+10*b+a=15664
1001*(a+d)+110*(b+c)=15664
Mà 110*(b+c) có tận cùng là 0
Nên 1001*(a+d) có tận cùng là 4
Nên a + d có tận cùng là 4
1001 * 4 = 4004 ( loại )
1001 * 14 = 14014 ( nhận )
Vậy a+c=14
Vậy a = 9 ; d = 5
14014+110*(b+c)=15664
110*(b+c)=1650
b+c=1650:110
b+c=15
Vậy a + b + c + d = 14 + 15 = 29
4) cho 3điểm A,B ,C bất kì và 1 điểm O khác điểm A,B,C .Có bao nhiêu tia gốc O và đi qua 1 trong3 điểm A,B,C
Có \(\frac{3.\left(3-1\right)}{2}=\frac{3.2}{2}=3\) (tia) mà có gốc O và đi qua 1 trong 3 điểm A, B, C
Đúng 0
Bình luận (0)
Từ điểm M nằm ngoài (O), kẻ tiếp tuyến MA với (O), (A là tiếp điểm). Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B ( B khác A). Kẻ đường kính AC của (O). Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E. a) CM: 4 điểm E,H,O,C cùng thuộc 1 đường tròn b) CM: Tam giác AMB cân c) CM: BE.BMBC.BO
Đọc tiếp
Từ điểm M nằm ngoài (O), kẻ tiếp tuyến MA với (O), (A là tiếp điểm). Từ A kẻ đường thẳng vuông góc với OM tại H và cắt (O) tại B ( B khác A). Kẻ đường kính AC của (O). Tiếp tuyến tại C của (O) cắt đường thẳng AB tại E. a) CM: 4 điểm E,H,O,C cùng thuộc 1 đường tròn b) CM: Tam giác AMB cân c) CM: BE.BM=BC.BO
a. Em tự giải
b.
\(\Delta OAB\) cân tại O (do \(OA=OB=R\), mà \(OH\) là đường vuông góc (do OH vuông góc AB)
\(\Rightarrow OH\) đồng thời là trung tuyến và trung trực của AB
Hay OM là trung trực của AB
\(\Rightarrow MA=MB\Rightarrow\Delta MAB\) cân tại M
c.
Do EC là tiếp tuyến tại C \(\Rightarrow EC\perp AC\)
MA là tiếp tuyến tại A \(\Rightarrow MA\perp AC\)
\(\Rightarrow EC||MA\Rightarrow\widehat{MAH}=\widehat{CEB}\) (so le trong)
Mà \(\widehat{MAH}=\widehat{MOA}\) (cùng phụ \(\widehat{AMH}\))
\(\Rightarrow\widehat{CEB}=\widehat{MOA}\)
Xét hai tam giác CEB và MOA có:
\(\left\{{}\begin{matrix}\widehat{CEB}=\widehat{MOA}\left(cmt\right)\\\widehat{CBE}=\widehat{MAO}=90^0\end{matrix}\right.\) \(\Rightarrow\Delta CEB\sim\Delta MOA\left(g.g\right)\)
\(\Rightarrow\dfrac{BE}{OA}=\dfrac{BC}{AM}\Rightarrow BE.AM=BC.OA\)
Mà \(MA=MB\) (theo cm câu b) và \(OA=BO=R\)
\(\Rightarrow BE.BM=BC.BO\)
Đúng 2
Bình luận (1)
a: Xét tứ giác EHOC có \(\widehat{EHO}+\widehat{ECO}=90^0+90^0=180^0\)
nên EHOC là tứ giác nội tiếp
=>E,H,O,C cùng thuộc một đường tròn
b: Ta có: ΔOAB cân tại O
mà OH là đường cao
nên OH là phân giác của góc AOB
Xét ΔAOM và ΔBOM có
OA=OB
\(\widehat{AOM}=\widehat{BOM}\)
OM chung
Do đó: ΔAOM=ΔBOM
=>MA=MB
=>ΔMAB cân tại M
c: Ta có: ΔAOM=ΔBOM
=>\(\widehat{OAM}=\widehat{OBM}=90^0\)
Xét tứ giác OAMB có \(\widehat{OAM}+\widehat{OBM}=90^0+90^0=180^0\)
nên OAMB là tứ giác nội tiếp
=>\(\widehat{OMB}=\widehat{OAB}=\widehat{CAB}\left(1\right)\)
Xét (O) có
\(\widehat{CAB}\) là góc nội tiếp chắn cung CB
\(\widehat{ECB}\) là góc tạo bởi tiếp tuyến CE và dây cung CB
Do đó: \(\widehat{CAB}=\widehat{ECB}\left(2\right)\)
Từ (1),(2) suy ra \(\widehat{OMB}=\widehat{ECB}\)
Xét ΔOMB và ΔECB có
\(\widehat{OMB}=\widehat{ECB}\)
\(\widehat{OBM}=\widehat{EBC}=90^0\)
Do đó: ΔOMB~ΔECB
=>\(\dfrac{BO}{BE}=\dfrac{BM}{BC}\)
=>\(BO\cdot BC=BM\cdot BE\)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời
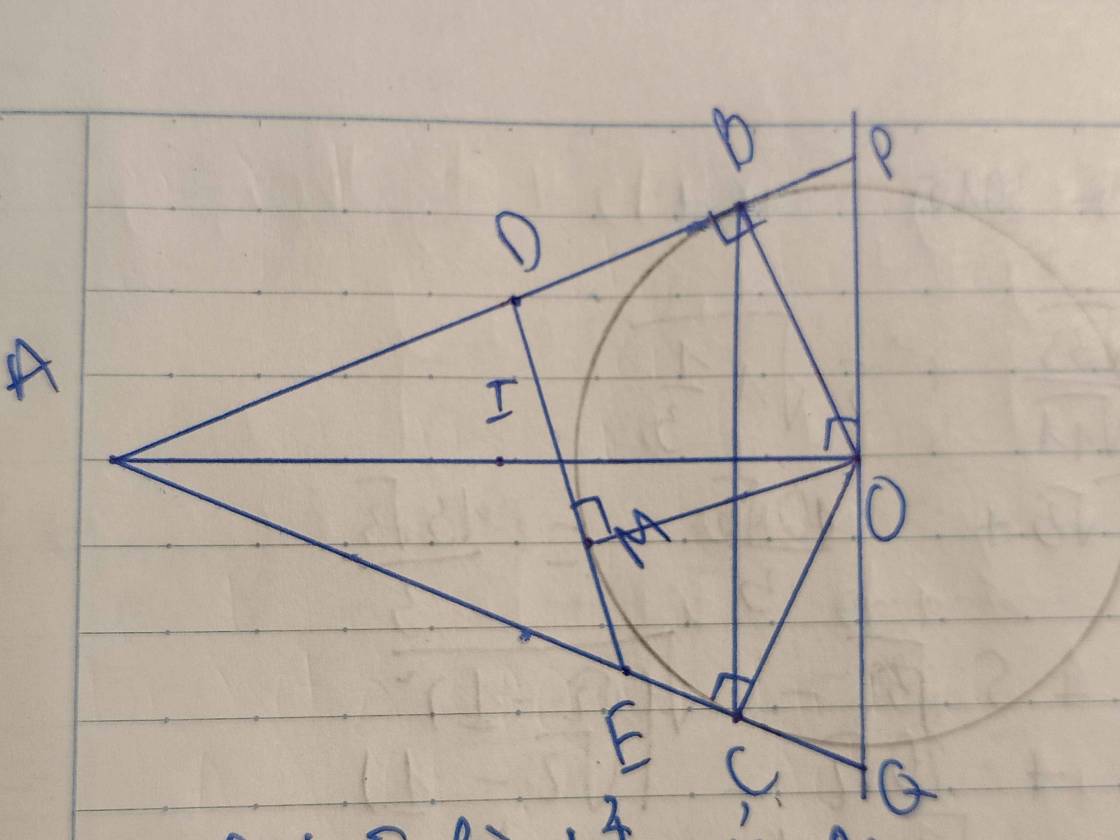
Cho 2 đường tròn (O,R) và (OR) cắt nhau tạo A và B ( O và O nằm khác phía với AB và góc OAO 90) Vẽ hình bình hành OAOEa) CM OEBO là hình bình hành (Cái này mình chứng minh đc r)b) Xác định tâm và bán kinh của đường tròn ngoại tiếp tam giác ABE ( câu này còn vế 2)c)Tiếp tuyến tại A của đường tròn (O) cắt (O) tại C(C khác A) tiếp tuyến tại A của đường tròn (O) cắt (O) tại D (D khác A) Gọi F là điểm đối xứng của A qua B. Chứng minh A,C,F,D cùng thuộc 1 đường tròn. d) Chứng minh S OAOB (OO^2+AB^2)/4
Đọc tiếp
Cho 2 đường tròn (O,R) và (OR') cắt nhau tạo A và B ( O và O' nằm khác phía với AB và góc OAO' >90) Vẽ hình bình hành OAO'E
a) CM OEBO' là hình bình hành (Cái này mình chứng minh đc r)
b) Xác định tâm và bán kinh của đường tròn ngoại tiếp tam giác ABE ( câu này còn vế 2)
c)Tiếp tuyến tại A của đường tròn (O') cắt (O) tại C(C khác A) tiếp tuyến tại A của đường tròn (O) cắt (O') tại D (D khác A) Gọi F là điểm đối xứng của A qua B. Chứng minh A,C,F,D cùng thuộc 1 đường tròn.
d) Chứng minh S OAO'B <=(OO'^2+AB^2)/4
Cho a,b khác o
CMR:\(\frac{a^2}{b^2}+\frac{b^2}{a^2}+4\ge3\left(\frac{a}{b}+\frac{b}{a}\right)\)
Lời giải :
Đặt \(\frac{a}{b}=t\Leftrightarrow\frac{b}{a}=\frac{1}{t}\)
BĐT \(\Leftrightarrow t^2+\frac{1}{t^2}+4\ge3\left(t+\frac{1}{t}\right)\)
\(\Leftrightarrow\left(t+\frac{1}{t}\right)^2-3\left(t+\frac{1}{t}\right)+2\ge0\)
\(\Leftrightarrow\left(t+\frac{1}{t}-1\right)\left(t+\frac{1}{t}-2\right)\ge0\)
\(\Leftrightarrow\frac{t^2-t+1}{t}\cdot\frac{t^2-2t+1}{t}\ge0\)
\(\Leftrightarrow\frac{\left(t^2-t+1\right)\left(t-1\right)^2}{t^2}\ge0\)( luôn đúng )
Dấu "=" xảy ra \(\Leftrightarrow t=1\Leftrightarrow\frac{a}{b}=1\Leftrightarrow a=b\)
Đúng 0
Bình luận (0)