Chứng minh với 2 cung nhỏ trong 1 đường tròn " 2 cung bằng nhau căng 2 dây bằng nhau "
Những câu hỏi liên quan
Chứng minh rằng trong 1 đường tròn, 2 cung bị chắn bởi 2 dây song song thì bằng nhau.
Gọi đường tròn Ở, 2 dây AB ss với CD
xet Tu giac ABCD co AD=AO+OD
CB=CO+OB
mà CO=OB=OA=OD
=> tu giac ABCD là hinh chu nhat
=>AOB=COD
=>cung CD=cungAB
Đúng 0
Bình luận (0)
1.Khoanh tròn vào mệnh đề sai:A. Trong một đường tròn, đường kính đi qua trung điểm của một dây cung thì chia cung căng dây ấy thành 2 phần bằng nhau.B. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.C. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.D. Trong một đường tròn, hai cung bị chắn bởi hai dây song song thì bằng nhau.2.Khoanh tròn vào khẳng định đúng...
Đọc tiếp
1.Khoanh tròn vào mệnh đề sai:
A. Trong một đường tròn, đường kính đi qua trung điểm của một dây cung thì chia cung căng dây ấy thành 2 phần bằng nhau.
B. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì vuông góc với dây căng cung ấy và ngược lại.
C. Trong một đường tròn, đường kính đi qua điểm chính giữa của một cung thì đi qua trung điểm của dây căng cung ấy.
D. Trong một đường tròn, hai cung bị chắn bởi hai dây song song thì bằng nhau.
2.Khoanh tròn vào khẳng định đúng:
A. Tứ giác có tổng hai góc bằng 1800 thì tú giác đó nội tiếp.
B. Tứ giác có bốn đỉnh cách đều 1 điểm O cho trước thì nội tiếp.
C. Tứ giác có hai đỉnh cùng nhìn cạnh chứa 2 đỉnh còn lại dưới một góc a thì nội tiếp.
D. Tứ giác có hai đỉnh cùng nhìn cạnh còn lại dưới một góc vuông thì nội tiếp.
E. Tứ giác có 1 góc bằng góc ngoài của góc đối diện thì nội tiếp.
cho đường tròn tâm O và 2 dây AB, CD bằng nhau và cắt nhau tại I, sao cho D thuộc cung nhỏ AB. chứng minh điểm O cách đều AD, BC
Cho (O) , 2 dây AB và CD bằng nhau và cắt nhau tại điểm I bên trong đường tròn.(C thuộc cung nhỏ AB). Chứng minh rằng :
a) OI là tia phân giác góc BOD
b) AI = CI và DI = IB
a) Cho đường tròn tâm O bán kính R. Hai dây AB và CD bằng nhau và vuông gócvới nhau tại I. Chứng minh rằng \(IA^2+IB^2+IC^2+ID^2\) không đổi.b) Trong đường tròn tâm O vẽ dây cung AD không đi qua O. Đường kính vuônggóc với OA cắt tiếp tuyến tại D của (O) tại điểm C. Chứng minh rằng phân giác của gócDCO song song với đường trung trực của AD
Cho đường tròn tâm O, 2 dây AB và CD bằng nhau và cắt nhau tại I sao cho D thuộc cung nhỏ AB. Chứng minh điểm O cách đều AD và CB.
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.Hình 29
Đọc tiếp
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
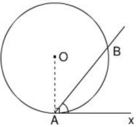
Hình 29
Cách 1: (Chứng minh trực tiếp)
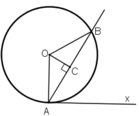
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
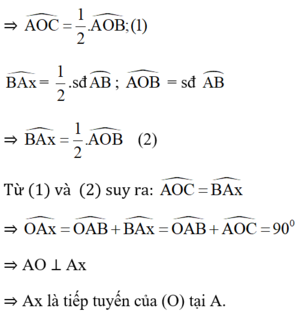
Cách 2: (Chứng minh phản chứng)
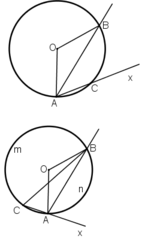
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB
+ C nằm trên cung lớn AB
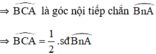
Mà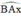 
là góc ngoài của tam giác BAC
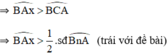
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.
Kiến thức áp dụng
+ Trong một đường tròn, số đo của góc nội tiếp bằng nửa số đo của cung bị chắn.
Đúng 0
Bình luận (0)
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.Hình 29
Đọc tiếp
Chứng minh định lí đảo của định lí về góc tạo bởi tia tiếp tuyến và dây cung , cụ thể là: Nếu góc BAx (với đỉnh A nằm trên đường tròn, một cạnh chứa dây cung AB), có số đo bằng nửa số đo của cung AB căng dây đó và cung này nằm bên trong góc đó thì cạnh Ax là một tia tiếp tuyến của đường tròn(h.29).
Gợi ý: có thể chứng minh trực tiếp hoặc chứng minh bằng phản chứng.
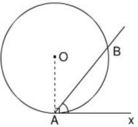
Hình 29
Cách 1: (Chứng minh trực tiếp)
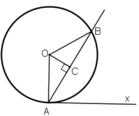
Gọi C là chân đường cao hạ từ O xuống AB.
ΔOAB có OA = OB = R nên tam giác này cân tại O
⇒ đường cao OC đồng thời là phân giác
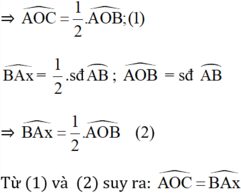
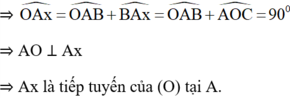
Cách 2: (Chứng minh phản chứng)
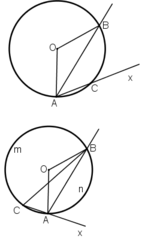
Giả sử Ax không phải tiếp tuyến của (O)
⇒ Ax là cắt (O) tại C khác A.
+ C nằm trên cung nhỏ AB
+ C nằm trên cung lớn AB
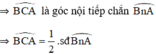
Mà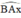 
là góc ngoài của tam giác BAC
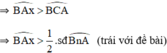
Vậy giả sử là sai ⇒ Ax là tiếp tuyến của đường tròn tâm O.
Đúng 0
Bình luận (0)
cho 2 đường tròn (O) và (o') bằng nhau cắt nhau tại A và B; kẻ dây AM của (O) và dây BN của (O') sao cho AM//BN. CMR cung nhỏ AM bằng cung nhỏ BN