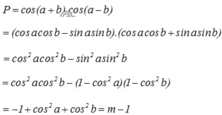Cho biết cosa=1/3 . Tinh cos2a

Những câu hỏi liên quan
Cho sina - cosa =1/5. Tính sin2a, cos2a
(Sina -cosa)^2 =1:25
<=> sin^2a +cos^2a -2sina.cosa =1:25
Ta có sin^2a+cos^2a = 1
<=> 1-2 sina.cosa =1:25
2sina.cosa =24:25
CT : sin2a= 2sina.cosa=24:25
Có sin^2 .2a + co^2.2a = 1
(24:25)^2 + cos^2.2a =1
Từ đây rút cos 2a = căn 1-(24:25)^2 =... bạn tự làm tiếp nha !
Đúng 0
Bình luận (0)
Câu 1: Biết a - b = \(\frac{\text{π}}{3}\). Tính giá trị biểu thức:
A = ( cosa + cosb )2 + ( sina + sinb )2
Câu 2: Cho biết cosa + sina = \(\frac{6}{5}\)và cosa > sina. Tính cos2a ; sin2a
\(A=cos^2a+cos^2b+2cosa.cosb+sin^2a+sin^2b+2sina.sinb\)
\(=cos^2a+sin^2a+cos^2b+sin^2b+2\left(cosa.cosb+sina.sinb\right)\)
\(=2+2cos\left(a-b\right)=2+2cos\frac{\pi}{3}=3\)
\(\left(cosa+sina\right)^2=\frac{36}{25}\Leftrightarrow1+2sina.cosa=\frac{36}{25}\)
\(\Rightarrow sin2a=\frac{36}{25}-1=\frac{11}{25}\)
\(cos2a=cos^2a-sin^2a=\left(cosa-sina\right)\left(cosa+sina\right)>0\)
\(\Rightarrow cos2a=\sqrt{1-sin^22a}=\frac{6\sqrt{14}}{25}\)
Đúng 0
Bình luận (0)
Cho \(\pi< \alpha< \dfrac{3\pi}{2}\) và sin a = \(\dfrac{-5}{13}\) . Tính cosa , sin2a , cos2a , và sin\(\dfrac{a}{2}\)
Lời giải:
$\sin ^2a+\cos ^2a=1$
$\cos ^2a=1-\sin ^2a=1-(\frac{-5}{13})^2=\frac{144}{169}$
Vì $\pi < a< \frac{3\pi}{2}$ nên $\cos a< 0$
Do đó: $\cos a=-\sqrt{\frac{144}{169}}=\frac{-12}{13}$
$\sin 2a=2\sin a\cos a=2.\frac{-5}{13}.\frac{-12}{13}=\frac{120}{169}$
$\cos 2a=\cos ^2a-\sin ^2a=2\cos ^2a-1=2.\frac{144}{169}-1=\frac{119}{169}$
$\cos a=\cos ^2\frac{a}{2}-\sin ^2\frac{a}{2}$
$=1-2\sin ^2\frac{a}{2}$
$\Leftrightarrow \frac{-12}{13}=1-2\sin ^2\frac{a}{2}$
$\Rightarrow \sin ^2\frac{a}{2}=\frac{25}{26}$
Vì $\pi < a< \frac{3\pi}{2}$ nên $\sin \frac{a}{2}>0$
$\Rightarrow \sin \frac{a}{2}=\frac{5}{\sqrt{26}}$
Đúng 0
Bình luận (0)
Don gian bieu thuc sau
a) A= \(\dfrac{1-cosa+cos2a}{sin2a-sina}\) b) B= \(\sqrt{\dfrac{1}{2}-\dfrac{1}{2}\sqrt{\dfrac{1}{2}+\dfrac{1}{2}cosa}}\) (0<a≤\(\pi\)).
c) C= \(\dfrac{cosa-cos3a+cos5a-cos7a}{sina+sin3a+sin5a+sin7a}\)
có A=\(\dfrac{1-cosa+2cos^2a-1}{2sina.cosa-sina}=\dfrac{cosa\left(2cosa-1\right)}{sina\left(2cosa-1\right)}=\dfrac{cosa}{sina}=cota\)
Đúng 2
Bình luận (0)
Cho cosa = 15/17 với 0 < a < Pi/2 . Tính sina , cos2a ?
Do \(0< a< \frac{\pi}{2}\Rightarrow sina>0\)
\(sin^2a+cos^2a=1\Rightarrow sina=\sqrt{1-cos^2a}=\sqrt{1-\left(\frac{15}{17}\right)^2}=\frac{8}{17}\)
\(cos2a=2cos^2a-1=2.\left(\frac{15}{17}\right)^2-1=\frac{161}{289}\)
Đúng 0
Bình luận (0)
Sử dụng định nghĩa tỉ số lượng giác của 1 góc nhọn để chứng minh rằng với góc nhọn a tùy ý ta có:
tan a=\(\dfrac{sina}{cosa}\) cot a=\(\dfrac{cosa}{sina}\) tan a . cot a =1 sin2a + cos2a= 1
Bài 1 CM các đẳng thức sau:
a, 1+ sin2a / sina + cosa - 1-tan ²a/2 / 1+ tan ²a/2 sina
b, cota - tana 2cot2a
c, 1+ cosa +cos2a + cos3a/ 2cos²a + cosa-1 2cosa
d, sin²a / sina- cosa - sina + cosa / tan²a sina + cosa
e, sin²a - cos²(a-b ) + 2coscosb ×cos(a-b) cos2a
f, cos²a - 2sina × ( 1-sina ) × cosa +( 1 + sina) × cosa - 2×(1+sina ) / 1- sina cosa
Bài 2 CM các đẳng thức sau ko phụ thuộc vào x
a, A sin⁶x + cos⁶x - 1 / sin⁴x + cos ⁴x -1
b, B ( 2sin ⁶x - 3sin ⁴x - 4...
Đọc tiếp
Bài 1 CM các đẳng thức sau:
a, 1+ sin2a / sina + cosa - 1-tan ²a/2 / 1+ tan ²a/2 = sina
b, cota - tana = 2cot2a
c, 1+ cosa +cos2a + cos3a/ 2cos²a + cosa-1 = 2cosa
d, sin²a / sina- cosa - sina + cosa / tan²a = sina + cosa
e, sin²a - cos²(a-b ) + 2coscosb ×cos(a-b) = cos2a
f, cos²a - 2sina × ( 1-sina ) × cosa +( 1 + sina) × cosa - 2×(1+sina ) / 1- sina = cosa
Bài 2 CM các đẳng thức sau ko phụ thuộc vào x
a, A= sin⁶x + cos⁶x - 1 / sin⁴x + cos ⁴x -1
b, B = ( 2sin ⁶x - 3sin ⁴x - 4sin²x ) +( 2cos⁶x - 3 cos⁴x- 4cos⁴x
c, C= sin⁴x + 3cos⁴x -1 / sin⁶x + cos⁶x + 3cos⁴x-1
Giải giúp tớ 2 bài này vs tớ cảm ơn nhìu
Cho các góc lượng giác a, b thỏa mãn
cos
2
a
+
cos
2
b
m
m
∈
ℝ
. Giá trị của biểu thức
P
cos
a
+
b
.
cos
a
-
b...
Đọc tiếp
Cho các góc lượng giác a, b thỏa mãn cos 2 a + cos 2 b = m m ∈ ℝ . Giá trị của biểu thức P = cos a + b . cos a - b là
A. P = m 2 - 1
B. P = 1 - m 2
C. P = m - 1
D. P = m + 1
Cho \(cosa=-\dfrac{2}{5}\) và \(\pi< a< \dfrac{3\pi}{2}\)
a) Tính các giá trị lượng giác còn lại của góc a
b) Giá trị biểu thức P = cos2a - cos\(\left(\dfrac{\pi}{3}-a\right)\)
b)\(P=cos2a-cos(\dfrac{\pi}{3}-a) \\=2cos^2a-1-cos\dfrac{\pi}{3}cosa-sin\dfrac{\pi}{3}sina \\=2.(\dfrac{-2}{5})^2-1-\dfrac{1}{2}.\dfrac{-2}{5}-\dfrac{\sqrt3}{2}.\dfrac{-\sqrt{21}}{5} \\=\dfrac{-24+15\sqrt7}{50}\)
Đúng 1
Bình luận (0)
a, Vì : \(\pi< a< \dfrac{3\pi}{2}\) nên \(cos\alpha< 0\) mà \(cos^2\alpha=1-sin^2\alpha=1-\dfrac{4}{25}=\dfrac{21}{25},\)
do đó : \(cos\alpha=-\dfrac{\sqrt{21}}{5}\)
từ đó suy ra : \(tan\alpha=\dfrac{2}{\sqrt{21}},cot\alpha=\dfrac{\sqrt{21}}{2}\)
Đúng 1
Bình luận (0)