Cho đg tròn (C) có tâm I thuộc trục Ox và đi qua 2 điểm M(1;-2), N(3;-1). Viết pt đg tròn (C)

Những câu hỏi liên quan
lập phương trình đường tròn đi qua 2 điểm M(1,2) ; N(-1,-1) và có tâm thuộc Ox
Đường tròn (C) đi qua hai điểm A(1;1); B (5; 3) và có tâm I thuộc trục hoành có phương trình là: A.
x
+
4
2
+
y
2
10.
B.
x
−
4
2
+
y
2
10.
C. ...
Đọc tiếp
Đường tròn (C) đi qua hai điểm A(1;1); B (5; 3) và có tâm I thuộc trục hoành có phương trình là:
A. x + 4 2 + y 2 = 10.
B. x − 4 2 + y 2 = 10.
C. x − 4 2 + y 2 = 10 .
D. x + 4 2 + y 2 = 10 .
cho nửa đg tròn tâm O có đg kính AB=2R.Trên tia tới của tia AB lấy điểm M bất kỳ từ M. Vẽ đg thẳng ko đi qua O,đg thẳng này cắt nửa đg tròn O tại C và D(C nằm giữa M và D).Gọi I là giao điểm của AD và BC vẽ IE vuông góc vs AB
a)CM:ΔMAD đồng dạng ΔMCB.Từ đó suy ra MA.MD=MC.MD
b)CM:tg BDIE nt
c)CM:DI là tia phân giác của góc CDE
a) Xét (O) có
\(\widehat{CDA}\) là góc nội tiếp chắn \(\stackrel\frown{CA}\)
\(\widehat{ABC}\) là góc nội tiếp chắn \(\stackrel\frown{CA}\)
Do đó: \(\widehat{CDA}=\widehat{ABC}\)(Hệ quả góc nội tiếp)
hay \(\widehat{MDA}=\widehat{MBC}\)
Xét ΔMAD và ΔMCB có
\(\widehat{MDA}=\widehat{MBC}\)(cmt)
\(\widehat{AMD}\) chung
Do đó: ΔMAD\(\sim\)ΔMCB(g-g)
Suy ra: \(\dfrac{MA}{MC}=\dfrac{MD}{MB}\)(Các cặp cạnh tương ứng tỉ lệ)
hay \(MA\cdot MB=MC\cdot MD\)(đpcm)
Đúng 2
Bình luận (1)
Cho góc xOy bằng 90 độ. Trên tia Ox lấy điểm I, Oy lấy điểm K. Đường tròn tâm I bán kính Ok cắt Ox tại M ( I nằm giữa O và M ). Đường tròn tâm K bán kính OI cắt Oy tại N ( K nằm giữa O và N).a, C/m: Đường tròn tâm I và đường tròn tâm K cắt nhau b, Tiếp tuyến tại M của đường tròn tâm I và tiếp tuyến tại N của đường tròn tâm K cắt nhau tại C. C/m: OMCN là hình vuôngc, Gọi giao điểm của 2 đường tròn tâm I và đường tròn tâm K là A và B. C/m: A,B,C thẳng hàng d, Giả sử I và K di động trên Ox là Oy s...
Đọc tiếp
Cho góc xOy bằng 90 độ. Trên tia Ox lấy điểm I, Oy lấy điểm K. Đường tròn tâm I bán kính Ok cắt Ox tại M ( I nằm giữa O và M ). Đường tròn tâm K bán kính OI cắt Oy tại N ( K nằm giữa O và N).
a, C/m: Đường tròn tâm I và đường tròn tâm K cắt nhau
b, Tiếp tuyến tại M của đường tròn tâm I và tiếp tuyến tại N của đường tròn tâm K cắt nhau tại C. C/m: OMCN là hình vuông
c, Gọi giao điểm của 2 đường tròn tâm I và đường tròn tâm K là A và B. C/m: A,B,C thẳng hàng
d, Giả sử I và K di động trên Ox là Oy sao cho Oy+OA = a (không đổi). C/m: AB luôn đi qua một điểm cố định.
Cho đường tròn tâm O bán kính R, đường thẳng a cắt đg tròn tại A và B. Gọi M thuộc a và nằm ngoài đg tròn. Qua M kẻ các tiếp tuyến MC; MD. Chứng minh
Khi M thay đổi trên a thì đg thẳng CD luôn đi qua điểm cố định
câu 1 :trong mp tọa độ Oxy cho 2 điểm A(-1;2) và B(5;4). giả sử có 1 con kiến đi từ A theo 1 đường thẳng đến 1 điểm M trên trục Ox, sau đó nó đi tiếp theo con đường thẳng từ M đến điểm B. Tìm tọa độ điểm M trên trục Ox để quãng đường mà con kiến đi từ A đến B là ngắn nhất.câu 2: cho đường thẳng d: 2x-y+20 và d: 2x-y-60. phép đối xứng tâm biến đường thẳng d thành d và biến trục Ox thành chính nó có tâm đối xứng là?câu 3 : trong mp oxy cho 3 điểm A(1;1) ,B(4;1) ,c(4;3) .phép quay tâm O góc quay...
Đọc tiếp
câu 1 :trong mp tọa độ Oxy cho 2 điểm A(-1;2) và B(5;4). giả sử có 1 con kiến đi từ A theo 1 đường thẳng đến 1 điểm M trên trục Ox, sau đó nó đi tiếp theo con đường thẳng từ M đến điểm B. Tìm tọa độ điểm M trên trục Ox để quãng đường mà con kiến đi từ A đến B là ngắn nhất.
câu 2: cho đường thẳng d: 2x-y+2=0 và d': 2x-y-6=0. phép đối xứng tâm biến đường thẳng d thành d' và biến trục Ox thành chính nó có tâm đối xứng là?
câu 3 : trong mp oxy cho 3 điểm A(1;1) ,B(4;1) ,c(4;3) .phép quay tâm O góc quay 90* biến tam giác ABC thành tam giác A'B'C' có tâm đường tròn ngoại tiếp là?
câu 4; trong mp Oxy cho đường thẳng d:2x+3y-3=0. ảnh của đt d qua phép vị tự tâm O tỉ số k=2 biến đường thẳng d thành đường thẳng có phương trình là?
cau5: cho các chữ cái dưới đây . có mấy chữ cái có trục đối xứng: A, B ,C ,D, Đ ,E, G, H, I ,K ,L?
câu này mà ở lớp 1 cả lớp 5 còn ko giải được.
mà hình như nó còn chẳng phải toán
Đúng 0
Bình luận (0)
Trong không giân với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(3;2;-3). Mặt cầu (S) có tâm I thuộc Ox và đi qua A, B có phương trình A.
x
2
+
y
2
+
z
2
-
8
x
+
2
0
B.
x
2
+
y
2
+
z
2...
Đọc tiếp
Trong không giân với hệ trục tọa độ Oxyz, cho điểm A(1;1;2), B(3;2;-3). Mặt cầu (S) có tâm I thuộc Ox và đi qua A, B có phương trình
A. x 2 + y 2 + z 2 - 8 x + 2 = 0
B. x 2 + y 2 + z 2 + 8 x + 2 = 0
C. x 2 + y 2 + z 2 - 4 x + 2 = 0
D. x 2 + y 2 + z 2 - 8 x + 2 = 0
Cho tứ giác ABCD có 4 đỉnh nằm trên đg tròn tâm O bán kính R sao cho AB,CD, BC, Da không qua O và đg thẳng AB cắ đg thẳng CD tại I, H là trung điểm AB, K là trung điểm Ab
1) O,H,I,K thuộc đg tròn tâm O
2) HK<OI
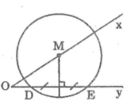
Cho góc nhọn xOy và hai điểm D, E thuộc tia Oy. Dựng đường tròn tâm M đi qua D và E sao cho tâm M nằm trên tia Ox.
* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).
Đúng 0
Bình luận (0)
















