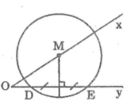
* Cách dựng:
- Dựng đường trung trực của DE cắt Ax tại M
- Dựng đường tròn tâm M bán kính MD
* Chứng minh:
Theo cách dựng ta có: M ∈ Ox
MD = ME (tính chất đường trung trực)
Suy ra: E ∈ (M; MD).
Cho góc nhọn xOy, điểm A thuộc tia Ox. Dựng đường tròn tâm I tiếp xúc với Ox tại A và có tâm I nằm trên Oy.
Cho góc xOy và tia Oz nằm giữa hai tia Ox và Oy sao cho góc xOz > góc zOy. Trên tia Ox lấy điểm A, trên tia Oz lấy điểm M sao cho góc OAM > 90 độ. Vẽ đường tròn tâm M bán kính MA. Tia Ox có điểm chung thứ 2 với đường tròn là B, tia Oy có 2 điểm chung với đường tròn là B, tia Oy có 2 điểm chung với đường tròn là C và D. So sánh độ dài của 2 đoạn thẳng AB và CD.
Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Cho góc nhọn xAy và hai điểm B, C thuộc tia Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Cho góc xOy bằng 90 độ. Trên tia Ox lấy điểm I, Oy lấy điểm K. Đường tròn tâm I bán kính Ok cắt Ox tại M ( I nằm giữa O và M ). Đường tròn tâm K bán kính OI cắt Oy tại N ( K nằm giữa O và N).
a, C/m: Đường tròn tâm I và đường tròn tâm K cắt nhau
b, Tiếp tuyến tại M của đường tròn tâm I và tiếp tuyến tại N của đường tròn tâm K cắt nhau tại C. C/m: OMCN là hình vuông
c, Gọi giao điểm của 2 đường tròn tâm I và đường tròn tâm K là A và B. C/m: A,B,C thẳng hàng
d, Giả sử I và K di động trên Ox là Oy sao cho Oy+OA = a (không đổi). C/m: AB luôn đi qua một điểm cố định.
Cho góc nhọn xAy và hai điểm B, C thuộc Ax. Dựng đường tròn (O) đi qua B và C sao cho tâm O nằm trên tia Ay.
Cho góc nhọn xOy và tia Oz nằm giữa hai tia Ox, Oy sao cho góc xOz lớn hơn góc zOy. Trên các tia Ox và Oz lần lượt lấy A và M sao cho góc OAM lớn hơn 90 độ. Vẽ đường tròn tâm M bán kính MA. Tia Ox và đường tròn (M) có điểm chung thứ hai là B. Tia Oy có hai điểm chung với đường tròn (M) là C và D. So sánh độ dài hai đoạn thẳng AB và CD.
Cho góc nhọn xOy. A,B thuộc tia Ox, C,D thuộc tia Oy. M là điểm nằm trong góc xOy sao cho S∆MAB=S∆MCD. Gọi E,F lần lượt là các điểm trên tia Ox, Oy sao cho OE=AB, OF=CD. Gọi I là trung điểm EF. Cmr: 3 điểm O, I, M thẳng hàng.
cho góc xOy vuông. trên Ox Oy lần lượt lấy hai điểm A và B sao OA=OB. M là điểm bất kỳ trên AB. Dựng đường tròn tâm O1 đi qua M và tiếp xúc với Ox tại A, đường tròn tâm O2 đi qua M và tiếp xúc nhiều với Oy tại B. cm tứ giác OANB nội tiếp và ON là phân giác của ANB
CM tứ
