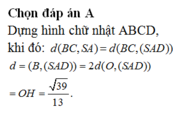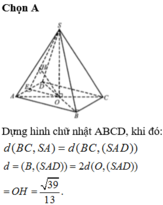Cho hình chóp tam giác đều S.ABC góc giữa hai đường thẳng SA và BC bằng

Những câu hỏi liên quan
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa đường thẳng SA với mặt phẳng (ABC) bằng
60
°
. Gọi G là trọng tâm của tam giác ABC, khoảng cách giữa hai đường thẳng GC và SA bằng A.
a
5
10
B.
a
5
5
C.
a
2...
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a và góc giữa đường thẳng SA với mặt phẳng (ABC) bằng 60 ° . Gọi G là trọng tâm của tam giác ABC, khoảng cách giữa hai đường thẳng GC và SA bằng
A. a 5 10
B. a 5 5
C. a 2 5
D. a 5
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng
60
0
. Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng.
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng 60 0 . Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng.
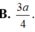
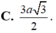
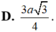
Chọn đáp án B

Gọi G là trọng tâm tam giác đều ABC, E là trung điểm của SA, K, H là hình chiếu của G, E lên SA.
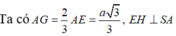
HE ⊥ BC vì HE là trung tuyến trong tam giác cân HBC.
Suy ra HE là đoạn vuông góc chung của SA và BC
![]()
Xét tam giác SAG vuông tại G. SG = tan 60 0 .AG = a
![]()
Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng
60
°
. Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng. A.
3
a
2
B.
3
a
4
C.
3
a
3
2
D....
Đọc tiếp
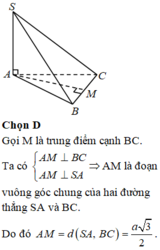
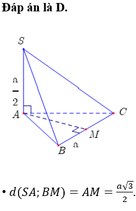
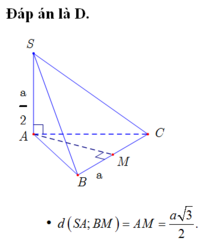
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng 60 ° . Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng.
A. 3 a 2
B. 3 a 4
C. 3 a 3 2
D. 3 a 3 4
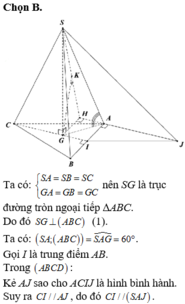
Chọn B.
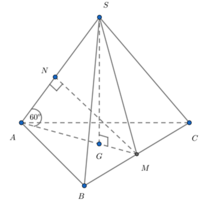
Phương pháp: Dựng đoạn vuông góc chung.
Cách giải: Gọi M là trung điểm BC, G là tâm của đáy, N là hình chiếu của M lên SA.

Đúng 0
Bình luận (0)
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng 60°. Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng.
Đọc tiếp
Cho hình chóp tam giác đều S.ABC có cạnh đáy bằng a. Góc hợp bởi cạnh bên và mặt phẳng đáy bằng 60°. Khi đó khoảng cách giữa hai đường thẳng SA và BC bằng.

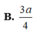
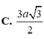
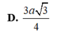
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và
S
A
a
2
. Tính khoảng cách giữa hai đường thẳng SA và BC A.
a
3
B. a C.
a
3
4
D.
a
3
2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt phẳng đáy và S A = a 2 . Tính khoảng cách giữa hai đường thẳng SA và BC
A. a 3
B. a
C. a 3 4
D. a 3 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a,SA vuông góc với mặt phẳng đáy và SA a. Tính khoảng cách giữa hai đường thẳng SA và BC A.
a
3
B. a C.
a
3
/4 D.
a
3
/2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a,SA vuông góc với mặt phẳng đáy và SA = a. Tính khoảng cách giữa hai đường thẳng SA và BC
A. a 3
B. a
C. a 3 /4
D. a 3 /2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, vuông góc với mặt phẳng đáy và SAa. Tính khoảng cách giữa hai đường thẳng SA và BC.
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, vuông góc với mặt phẳng đáy và SA=a. Tính khoảng cách giữa hai đường thẳng SA và BC.
![]()
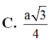
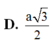
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
A
B
1
,
B
C
3
, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA, BC bằng
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 1 , B C = 3 , mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA, BC bằng
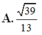
![]()
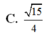
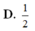
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B,
A
B
1
,
B
C
3
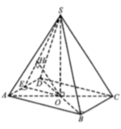
, mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA, BC bằng A.
39
13
B. 1 C.
15
4
D. 2
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông tại B, A B = 1 , B C = 3 , mặt bên SAC là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Khoảng cách giữa hai đường thẳng SA, BC bằng
A. 39 13
B. 1
C. 15 4
D. 2
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh
a
,
S
A
⊥
A
B
C
,
góc giữa đường thẳng SB và mặt phẳng
A
B
C
bằng
60
°
.
Khoảng cách giữa hai đường thẳng AC và SB bằng: A.
a
2...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a , S A ⊥ A B C , góc giữa đường thẳng SB và mặt phẳng A B C bằng 60 ° . Khoảng cách giữa hai đường thẳng AC và SB bằng:
A. a 2 2
B. 2 a
C. a 15 5
D. a 7 7
Đáp án C

S A ⊥ A B C ⇒ A B là hình chiếu vuông góc của SB lên A B C
⇒ S B , A B C ^ = S B , A B ^ = S B A ^ = 60 ° ⇒ S A = A B . tan 60 ° = a 3
Dựng d qua B và d / / A C
Dựng A K ⊥ d tại K
Dựng A H ⊥ S K tại H
Ta có B K ⊥ A K B K ⊥ S A ⇒ B K ⊥ S A K ⇒ B K ⊥ A H
+ B K ⊥ A H S K ⊥ A H ⇒ A H ⊥ S B K ⇒ d A , S B K = A H
+ B K / / A C S K ⊂ S B K A C ⊄ S B K ⇒ A C / / S B K ⇒ d A C , S B = d A , S B K = A H
Gọi M là trung điểm A C ⇒ B M ⊥ A C 1 ; B K ⊥ A K B K / / A C ⇒ A K ⊥ A C 2
1 , 2 ⇒ A K / / B M ⇒ A K B M là hình bình hành ⇒ A K = B M = a 3 2
Xét tam giác SAK vuông tại A ta có 1 A H 2 = 1 A K 2 + 1 S A 2 = 5 3 a 2 ⇒ A H = a 15 5
Vậy d A C , S B = a 15 5
Đúng 0
Bình luận (0)