cho đoạn thẳng ab cố định c là điểm di động trên AB. Vẽ về một phía của đoạn thẳng AB các nửa đường tròn có đường kính AB,BC,AC. Xác định vị trí C để diện tích phần giới hạn bởi 3 đường tròn đạt GTLN

Những câu hỏi liên quan
Cho đoạn thẳng AB và điểm C di dộng trên đó. Trên cùng 1 nửa mặt phẳng bờ AB vẽ các nửa đường tròn có các đường kính AB,AC,BC. Xác định vị trí của điểm C để diện tích cắt bởi các nửa đường tròn có GTLN.
Cho đoạn thẳng AB, điểm C nằm giữa AB. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, BC. Đường vuông góc với AB tại C cắt nửa đường tròn lớn hơn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, BC theo thứ tự tại M, N. Điểm C ở vị trí nào trên AB thì MN có độ dài lớn nhất.
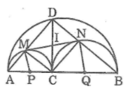
Gọi O là trung điểm của AB
Tứ giác CMDN là hình chữ nhật nên CD = MN
Trong tam giác OCD ta có: CD ≤ OD nên MN ≤ OD
Vì OD không đổi nên MN = OD là giá trị lớn nhất khi và chỉ khi C trùng với O
Vậy C là trung điểm của AB thì MN có độ dài lớn nhất.
Đúng 0
Bình luận (0)
Cho nửa đường tròn đường kính AB . điểm C di động trên nửa đường tròn . Kéo dài AC 1 đoạn CF = BC . Tìm tập hợp điểm F , xác định Vị trí của C trên nửa đường tròn sao cho chu vi tam giác ABC max
Cho đường tròn tâm O, bán kính R. AB là 1 dây cung cố định và AB R nhân căn 3. M là trung điểm của AB. C là điểm chuyển động trên cung AB. I là trung điểm của AC. H là hình chiếu của I trên BCa. Cmr: Điểm I thuộc đường tròn bán kính OBb. Tính góc AOB và độ dài đoạn thẳng OM theo Rc. Cmr: I thuộc 1 đường cố địnhd. Cmr: Đường thẳng IH đi qua 1 điểm cố địnhe. Cmr: H thuộc 1 đường thẳng cố địnhf. Xác định vị trí điểm C sao cho diện tích OBCA lớn nhất
Đọc tiếp
Cho đường tròn tâm O, bán kính R. AB là 1 dây cung cố định và AB = R nhân căn 3. M là trung điểm của AB. C là điểm chuyển động trên cung AB. I là trung điểm của AC. H là hình chiếu của I trên BC
a. Cmr: Điểm I thuộc đường tròn bán kính OB
b. Tính góc AOB và độ dài đoạn thẳng OM theo R
c. Cmr: I thuộc 1 đường cố định
d. Cmr: Đường thẳng IH đi qua 1 điểm cố định
e. Cmr: H thuộc 1 đường thẳng cố định
f. Xác định vị trí điểm C sao cho diện tích OBCA lớn nhất
Cho đường tròn (O;R), đường kính AB. Lấy điểm M trên đoạn thẳng OA, đường thẳng qua M vuông góc với AB cắt đường tròn (O) tại C. Gọi D là điểm chính giữa của cung AB(C và D nằm khác phía đối với AB). Xác định vị trí của điểm M để diện tích tam giác MCD lớn nhất.
1) Cho đường tròn (O) đường kính AB 2R. Lấy điểm C di động trên đường tròn (O), gọi I là tâm đường tròn nội tiếp tam giác ABC, vẽ CH vuông góc AB tại H. a) Vẽ CM song song BI ( M thuôc đường thẳng AI). Trên đoạn thẳng AB lấy điểm F sao cho AC AF. Tính số đo góc CMF.b) Gọi K là tâm đường tròn nội tiếp tam giác CHA, CK cắt AB tại E. Tính giá trị lớn nhất của diện tích tam giác CEF theo R khi C di động trên (O). c) Chứng minh ba đường thẳng MH, CF và BI đồng qui tại một điểm.2) Cho tam giác nhọn...
Đọc tiếp
1) Cho đường tròn (O) đường kính AB = 2R. Lấy điểm C di động trên đường tròn (O), gọi I là tâm đường tròn nội tiếp tam giác ABC, vẽ CH vuông góc AB tại H.
a) Vẽ CM song song BI ( M thuôc đường thẳng AI). Trên đoạn thẳng AB lấy điểm F sao cho AC = AF. Tính số đo góc CMF.
b) Gọi K là tâm đường tròn nội tiếp tam giác CHA, CK cắt AB tại E. Tính giá trị lớn nhất của diện tích tam giác CEF theo R khi C di động trên (O).
c) Chứng minh ba đường thẳng MH, CF và BI đồng qui tại một điểm.
2) Cho tam giác nhọn ABC (AB < AC) nội tiếp đường tròn (O;R). Gọi M là điểm di động trên cung nhỏ BC. Vẽ AD vuông góc với MB tại D, AE vuông góc với MC tại E. Gọi H là giao điểm của DE và BC.
a) Chứng minh A, H,E cùng thuộc một đường tròn. Từ đó suy ra DE luôn đi qua một điểm cố định.
b) Xác định vị trí của M để MB/AD×MC/AE đạt giá trị lớn nhất.
Mọi người giúp em với ạ.
Cho đoạn thẳng AB và một điểm C trên đoạn AB. Vẽ trên cùng một nửa mặt phẳng bờ AB các nửa đường tròn có đường kính AB, AC, BC. Xác định vị trí của điểm C trên đoạn AB để diện tích phần giới hạn bởi ba nửa đường tròn đạt giá trị lớn nhất.
Cho điểm C thuộc đoạn AB, . Vẽ về môt phía của AB các nửa đường tròn có đường kính theo thứ tự là AC, AB. Tính bán kính của đường tròn (I) tiếp xúc với các nửa đường tròn trên và tiếp xúc với đoạn thẳng AB
mik chỉ cần câu hỏi thêm thui ko cần lời giải cho bài này đâu nha
Đúng 0
Bình luận (0)
Cho đoạn thẳng AB, điểm C nằm giữa AB. Vẽ về một phía của AB các nửa đường tròn có đường kính theo thứ tự là AB, AC, BC. Đường vuông góc với AB tại C cắt nửa đường tròn lớn hơn tại D. DA, DB cắt các nửa đường tròn có đường kính AC, BC theo thứ tự tại M, N. Chứng minh rằng MN là tiếp tuyến chung của các nửa đường tròn có đường kính AC, BC
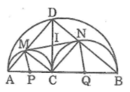
Gọi P là trung điểm của AC, Q là trung điểm của BC, I là giao điểm của MN với DC
Vì CMDN là hình chữ nhật nên IC = IM = ID = IN
Tam giác CNI cân tại I nên ![]() (3)
(3)
Tam giác CNQ cân tại Q nên ![]() (4)
(4)
Vì AB ⊥ CD nên ![]() =
90
°
(5)
=
90
°
(5)
Từ (3), (4) và (5) suy ra: ![]() =
90
°
hay MN ⊥ QN
=
90
°
hay MN ⊥ QN
Vậy MN là tiếp tuyến của đường tròn đường kính BC
Tam giác CMI cân tại I nên 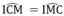 (6)
(6)
Tam giác CMP cân tại P nên 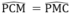 (7)
(7)
Vì AB ⊥ CD nên 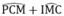 =
90
°
(8)
=
90
°
(8)
Từ (6), (7) và (8) suy ra: 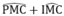 =
90
°
hay MN ⊥ PM
=
90
°
hay MN ⊥ PM
Vậy MN là tiếp tuyến của đường tròn đường kính AC
Đúng 0
Bình luận (0)









