hình tự vẽ nha bạn 

TAM GIÁC ABC có: BAM=CAM (GT)

Suy ra: AB/AC=MB/MC

Thay số vào ta được:24/32=15/MC

                              = 3/4=15/MC

                              => MC=20 cm

Vì AM là đường trung tuyến của tam giác ABC nên suy ra :

\(\frac{AB}{AC}=\frac{MB}{MC}\Rightarrow\frac{24}{32}=\frac{15}{MC}\Rightarrow MC=\frac{32.15}{24}=20\)cm 

Vậy MC = 20 cm 

xét tam giác BAM vuông tại M =>  Bm^2+ AM^2=AB^2 (định lý pytago)

                                                => 8^2+Am^2=10^2 => AM^2=36=6^2

xét tam giác BMC vuông tại M  => BM^2 +MC^2 = BC^2

                                                 => 8^2 + 15^2 =BC^2

                                                 => BC^2= 17^2

=> AC=21 . tam giác abc: AB^2+BC^2ko bằng AC^2

=> tam giác abc ko vuông

Xét `Delta ABC ` ta có

`AM` là tia phân giác của `hat(BAC)`

`=> (BM)/(CM) = (AB)/(AC)`

`=> CM = (BM*AC)/(AB)`

Mà `AB =12cm,AC=15cm,BM=8cm`

`=> CM=(8*15)/12=10(cm)`

Chọn A

Chọn đáp án A

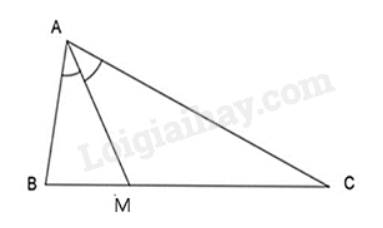
Vì \(AM\) là tia phân giác góc \(A\left( {M \in BC} \right)\) nên theo tính chất đường phân giác ta có:

\(\frac{{BM}}{{CM}} = \frac{{AB}}{{AC}};\frac{{BM}}{{AB}} = \frac{{CM}}{{AC}};\frac{{CM}}{{BM}} = \frac{{AC}}{{AB}};\frac{{AC}}{{CM}} = \frac{{AB}}{{BM}}\).

Câu 1)

A )Ta có tam giác ABC cân tại A 

=> \(\widehat{ABC}=\widehat{ACB}\)

Và AB = AC

Xét hai tam giác vuông BCK và CBH ta có :

BC chung

\(\widehat{KBC}=\widehat{BCH}\)

=>BCK = CBH (cạnh huyền - góc nhọn )

=>BH = CK (đpcm)

B) ta có BCK = CBH

=> \(\widehat{HBC}=\widehat{KCB}\)

=> \(\widehat{ABH}=\widehat{ACK}\)

=> tam giác OBC cân tại O

=> BO = CO

Xét tam giác ABO và tam giác ACO 

AB = AC

BO = CO (cmt)

\(\widehat{ABH}=\widehat{ACK}\)

=> ABO=ACO (c-g-c)

=> \(\widehat{BAO}=\widehat{CAO}\)

=> AO là phân giác góc ABC (đpcm)

C) ta có

AI là phân giác góc ABC 

Mà tam giác ABC cân tại A

=> AI vuông góc với cạnh BC (đpcm)

Xét t/g BAM và t/g DAM:

AB=AD(gt)

BAM=DAM(gt)

AM chung (gt)

Do đó t/g BAM= DAM(c.g.c)

Suy ra BM=DM( cặp cạnh tương ứng)

Vì góc MAD+AMD = MDC(t/c góc ngoài)

Suy ra MC lớn nhất trong t/g MDC

Hay DM<MC mà BM=DM nên BM<MC

Xét tam giác BAM và tam giác DAM có:

AB=AD(gt)

góc BAM= góc DAM(gt)

AM cạnh chung

Suy ra tam giác BAM= tam giác DAM(c-g-c)

Suy ra BM=DM(hai cạnh tương ứng)

Vì góc MAD+ góc AMD= góc MDC(t/c góc ngoài)

SUy ra MC là cạnh lớn nhất trong tam giác MDC

Hay DM<MC mà BM=DM nên BM<MC

đề sai rồi

BM sao cắt CM tại K được??

Đề sai rồi bạn

Xét tam giác ABC có 

AM là phân giác 

BM = MC => AM là trung tuyến 

Vậy tam giác ABC cân tại A => AB = AC 

bằng nhau theo trường hợp gì vậy  bạn