Cho tam giác ABC vuông tại A. Trên AC lấy M sao cho AM<MC. Vẽ đường tròn (O) đường kính CM, đường thẳng BM cắt (O) tại D, AD kéo dài cắt (O) tại S.
a,CM: BADC là tức giác nội tiếp.
b,

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB=5cm,AC=4cm. Trên AB lấy M sao cho AM=3cm,trên AC lấy N sao cho AN=1cm, trên BC lấy E sao cho BE=2/3 CE. Tính S tam giác ABC,AMN,CNE,MEN
CHO TAM GIÁC ABC VUÔNG TẠI A , AB= 3CM ,AC=2CM, BC= 5CM ,TRÊN AB LẤY M SAO CHO AM =2CM,TRÊN AC LẤY N SAO CHO AN=1CM, TRÊN BC LẤY E SAO CHO BE= 2,5. TÍNH HÌNH TAM GIÁC MNE
Cho tam giác ABC vuông tại A gọi M là trung điểm của AC. Trên tia AM lấy D sao cho AM=MD
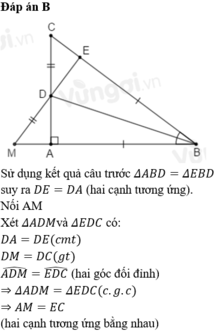
Cho tam giác ABC cân tại A. Trên AB lấy điểm M, trên AC lấy điểm N sao cho AM = AN; gọi I là giao điểm của NB và MC. Chứng minh: tam giác ANB = tam giác AMC Cho tam giác ABC cân tại A .Trên AB lấy điểm M, trên AC lấy điểm N sao cho AM=AN;gọi I là giao điểm của NB và MC
a) Chứng minh: tam giác ANB = tam giác AMC
b) Chứng minh: MN // BC
c) Gọi D là trung điểm của BC .Chứng minh:A ,I ,D thẳng hàng
cả hình nữa nha
Xem chi tiết
a,Xét tam giác ABN và tam giác ACM có :
AM=AN (gt)
Góc A chung
AB=AC(gt)
=> tam giác ABN = tam giác ACM (c-g-c)
b,theo câu a =>AMC^=ANB^(1)
Ta có : AM=AN =>tam giác AMN cân tại A => AMN^=ANM^(2)
Từ 1 và 2 =>MNI^=NMI^(3)
Vì B1^=C1^
B^=C^
=>B^-B1^=C-C1^
=>C2^=B2^(4)
Mặt khác : I1^=I2^(đối đỉnh) (5)
Từ 3 ; 4 và 5 => MNI^+NMI^+I1^=180*=I2^+B2^+C2^(tổng 3 góc của 1 tam giác )
=> MNI^+NMI^ / 2 = B2^+C2^ / 2
=> B2^=MNI^
Vì 2 góc này ở vị trí sole trong và bằng nhau
=> MN // BC
Đúng 2
Bình luận (0)
Tam giác ABC vuông tại A có AB=10cm,AC=20=cm. Trên AC lấy M sao cho AM=5cm
A.tính độ dài BC,BM
B. Chứng minh tam giác ABC~tam giác AMB
a: \(BC=10\sqrt{5}\left(cm\right)\)
\(BM=\sqrt{10^2+5^2}=5\sqrt{5}\left(cm\right)\)
b: Xét ΔABC vuông tại A và ΔAMB vuông tại A có
AB/AM=AC/AB
nên ΔABC∼ΔAMB
Đúng 1
Bình luận (0)
Cho tam giác ABC vuông tại A. Tia phân giác của góc ABC cắt AC tại D, lấy E trên BC sao cho BE=AB
Trên tia đối của tia DE lấy điểm M sao cho. So sánh EC và AM
A. EC<AM
B. EC=AM
C. EC>AM
D. Chưa đủ điều kiện để so sánh
cho tam giác ABC vuông tại A ( AC<AB) lấy M thuộc AB sao cho AM=AC . trên tia AC lấy D sao cho AD=AB vẽ AE vuông góc với BC ( E thuộc BC ) . tia AE cắt DM tại F
a) DM=CB
b) tam giác AFD , tam giác AMF tam cân
GIÚP MÌNH CÂU b VỚI MN
Cho tam giác ABC vuông cân tại A. Trên AB lấy M, trên tia đối của AC lấy N sao cho AM=AN . C/m rằng: BN vuông góc với CN
BN vuông góc CM nhé!
Vẽ hình ra trc khi đọc nha bạn như thế dễ hiểu hơn đấy!
Tam giác ABC vuông cân => góc ABC = ACB = 45 độ
Vì AN = AM, AB vuông góc AC => tam giác ANM vuông cân => góc ANM = AMN = 45 độ
=> góc ANM = BAC = 45 độ => ANM + BAC = 90 độ => NM vuông góc BC
Trong tam giác BNC có AB; NM là đường cao.
Mà Ab giao NM ở M => M là trực tâm tam giác BNC => CM vuông góc BN (đpcm)
Xong...
Đúng 0
Bình luận (0)
cho tam gsc ABC vuông tại A, đường cao AH. kẻ đường phân giác góc B của tam giác ABC cắt AH tại E . trên AB lấy M, trên AC lấy N sao cho AM/AB=CN/AC. CMR góc NHM = 90 độ
cho tam giác abc vuông tại a (ABAC) trung tuyết AM, Trên AM lấy D sao cho m là trung điểm của AD a) c/m tứ giác ABDC là hcn b) vẽ E dối xứng qua BC. c/m AE vuông góc ED c) c/m tư g...
Đọc tiếp
cho tam giác abc vuông tại a (AB<AC) trung tuyết AM, Trên AM lấy D sao cho m là trung điểm của AD a) c/m tứ giác ABDC là hcn b) vẽ E dối xứng qua BC. c/m AE vuông góc ED c) c/m tư giác BCDE là hình thang cân
a: Xét tứ giác ABDC có
M là trung điểm của AD
M là trung điểm của BC
Do đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Đúng 0
Bình luận (2)