giải bất phương trình sau:
-3x-1<8
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
1.Giải các phương trình sau : a,7x+35=0 b, 8-x/x-7 -8 =1/x-7 2.giải bất phương trình sau : 18-3x(1-x)_< 3x^2-3x
a: 7x+35=0
=>7x=-35
=>x=-5
b: \(\dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\)
=>8-x-8(x-7)=1
=>8-x-8x+56=1
=>-9x+64=1
=>-9x=-63
hay x=7(loại)
a, \(7x=-35\Leftrightarrow x=-5\)
b, đk : x khác 7
\(8-x-8x+56=1\Leftrightarrow-9x=-63\Leftrightarrow x=7\left(ktm\right)\)
vậy pt vô nghiệm
2, thiếu đề
1.
\(a,7x+35=0\\ \Rightarrow7x=-35\\ \Rightarrow x=-5\\ b,ĐKXĐ:x\ne7\\ \dfrac{8-x}{x-7}-8=\dfrac{1}{x-7}\\ \Leftrightarrow\dfrac{8-x}{x-7}-\dfrac{8\left(x-7\right)}{x-7}-\dfrac{1}{x-7}=0\\ \Leftrightarrow\dfrac{8-x-8x+56-1}{x-7}=0\\ \Rightarrow-9x+63=0\\ \Leftrightarrow-9x=-63\\ \Leftrightarrow x=7\left(ktm\right)\)
2.đề thiếu
Giải các bất phương trình sau: 1 2 log 1 3 x 2 - 3 x + 1 < 1
Điều kiện 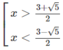
Vì 0 < 0,5 < 1 và 1 = 0 , 5 0 nên ta có:
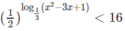
⇔ log 1 3 ( x 2 - 3 x + 1 ) > 0
⇔ x 2 − 3x + 1 > 1 ⇔ 0 < x < 3
Kết hợp với điều kiện, ta được nghiệm của bất phương trình đã cho là
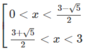
Giải bất phương trình sau: 3x^3-4x-1>=0
\(\Leftrightarrow3x^3-3x+x-1\ge0\\ \Leftrightarrow3x\left(x-1\right)\left(x+1\right)+\left(x-1\right)\ge0\\ \Leftrightarrow\left(x-1\right)\left(3x^2+3x+1\right)\ge0\\ \Leftrightarrow x-1\ge0\left(3x^2+3x+1=3\left(x+\dfrac{1}{2}\right)^2+\dfrac{1}{4}>0\right)\\ \Leftrightarrow x\ge1\)
Giải bất phương trình sau: 3 x + 1 2 - x - 2 3 < 1 - 2 x 4
Tập xác định D = R.
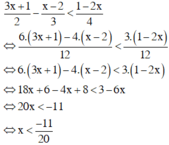
Vậy tập nghiệm của bất phương trình là 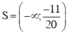
Giải bất phương trình sau log 1 5 ( 3 x - 5 ) > log 1 5 ( x + 1 )
![]()
![]()
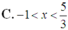
![]()
Giải các bất phương trình sau:
x + x > 2 x + 3 x - 1
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
Giải các bất phương trình sau: 1 x + 1 + 2 x + 3 < 3 x + 2
Giải bất phương trình sau: (3x-1)(x+2)>0?
Vì (3x-1)(x+2)>0
=> (3x-1) và (x+2) cùng dấu
Xét trường hợp (3x-1) và (x+2) cùng dương
3x+1>0=> x>-1/3
và x+2>0=> x>-2
Xét trường hợp (3x-1) và (x+2) cùng âm
3x+1<0=> x<-1/3
và x+2<0=> x<-2
từ 2 TH trên => x>-1/3 và x<-2
Vì ( 3x -1 )( x + 2 ) > 0
=> ( 3x-1) và (x+2) cùng dấu
Xét trường hợp (3x-1) và (x+2) cùng dương
3x+1 > 0 => x > (-1/3 )
và x+2 > 0=> x > ( -2 )
Xét trường hợp (3x-1) và (x+2) cùng âm
3x+1 < 0 => x < (-1/3 )
và x+2 < 0 => x < (-2)
từ 2 TH trên => x > (-1/3 ) và x < (-2)
Theo đề ta có :
\(\left(3x-1\right)\left(x+2\right)>0\)
\(\Rightarrow3x-1< 0\)\(;x+2< 0\) hoặc \(3x-1>0\) \(;\) \(x+2>0\)
\(\Rightarrow3x< 1\)\(;x< -2\) hoặc \(3x>1\)\(;x>-2\)
\(\Rightarrow x< \frac{1}{3};x< -2\) hoặc \(x>\frac{1}{3};x>-2\)
\(\Rightarrow x< -2\) hoặc \(x>\frac{1}{3}\) thì (3x-1)(x+2) >0
nha bn,Le Nhat Phuong!