Cho hàm số \(y=3sin2x+4cos2x+12x\). Giải phương trình \(y^{'}=2\)
Những câu hỏi liên quan
Giải các phương trình sau 4 cos 2 x - 3 sin x . cos x + 3 sin 2 x = 1
4 cos 2 x - 3 sin x . cos x + 3 sin 2 x = 1
Rõ ràng cosx ≠ 0, chia hai vế của phương trình cho cos2x ta được:
4 - 3 tan x + 3 tan 2 x = 1 + tan 2 x ⇔ 2 tan 2 x - 3 tan x + 3 = 0
Phương trình cuối vô nghiệm đối với tanx, do đó phương trình đã cho vô nghiệm
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau
y
2
s
i
n
2
x
+
3
s
i
n
2
x
-
4
c
o
s
2
x
A. miny -
3
2
-1;maxy
3
2
+1 B. miny -
3
2
-1;maxy ...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau y = 2 s i n 2 x + 3 s i n 2 x - 4 c o s 2 x
A. miny= - 3 2 -1;maxy= 3 2 +1
B. miny= - 3 2 -1;maxy= 3 2 -1
C. miny= - 3 2 ;maxy= 3 2 -1
D. miny= - 3 2 -2;maxy= 3 2 -1
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
3
sin
2
x
+
cos
2
x
sin
2
x
+...
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin 2 x + cos 2 x sin 2 x + 4 cos 2 x + 1
A.
B. 
C. 
D. 
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
3
sin
2
x
-
4
cos
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + 3 sin 2 x - 4 cos 2 x
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y
3
sin
2
x
+
cos
2
x
s
i
n
2
x
+
4
c
o
s
2...
Đọc tiếp
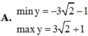
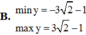
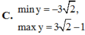
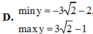
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số y = 3 sin 2 x + cos 2 x s i n 2 x + 4 c o s 2 x + 1
A. m i n y = - 5 - 65 4 , m a x y = - 5 + 65 4
B. m i n y = - 5 - 65 2 , m a x y = - 5 + 65 2
C. m i n y = - 5 - 3 5 4 , m a x y = - 5 + 3 5 4
D. m i n y = - 5 - 3 5 2 , m a x y = - 5 + 3 5 2
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau:
y
2
sin
2
x
+
3
sin
2
x
-
4
cos
2
x
Đọc tiếp
Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số sau: y = 2 sin 2 x + 3 sin 2 x - 4 cos 2 x
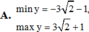
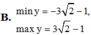
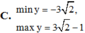
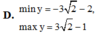
Tìm GTLN, GTNN của hàm số y = √(1−2sinx)
Giải phương trình lượng giác
a) sin4x + cos4x + sin4x = 1
b) tan2x + cotx = 4cos2x
Phương trình 3 sin 2 x + m sin 2 x – 4 cos 2 x = 0 có nghiệm khi:
A. m = 4
B. m ≥ 4
C. m ≤ 4
D. m ∈R
Cho hàm số y=2x^3+3x^2-2. Viết phương trình tiếp tuyến của đồ thị hàm số biết hệ số góc tiếp tuyến là k=12. A. y= 12x - 9 hoặc y= 12x +18 B. y= 12x - 9 hoặc y= 12x + 30 C. y= 12x + 15 hoặc y= 12x + 30 D. y= 12x + 15 hoặc y= 12x + 18
