cho tam giác ABC đều , cạnh là a . I,K,M lần lượt là trung điểm của AB,AC,BC
a) chứng mình : tứ giác BIKM là hình thoi
b) các tam giác : AIK,KMC, là tam giác đều
c) tính diện tích hình thoi BIKM và tam giác AIK, KMc
Những câu hỏi liên quan
Cho tam giác ABC có 3 góc nhọn và ABAC. Đường tròn tâm O đường kính AB 2R cắt cạnh BC,AC lần lượt tại I,K. Tiếp tuyến của đường tròn O tại B cắt AI tại D, H là giao điểm của AI và BKa, Chứng minh tứ giác IHKC nội tiếpb, Chứng minh BC là tia phân giác của góc DBH và tứ giác BDCH là hình thoic, Tính diện tích hình thoi BDCH theo R trong trường hợp tam giác ABC đềugiúp vs ạ
Đọc tiếp
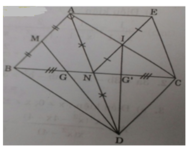
Cho tam giác ABC có 3 góc nhọn và AB=AC. Đường tròn tâm O đường kính AB =2R cắt cạnh BC,AC lần lượt tại I,K. Tiếp tuyến của đường tròn O tại B cắt AI tại D, H là giao điểm của AI và BK
a, Chứng minh tứ giác IHKC nội tiếp
b, Chứng minh BC là tia phân giác của góc DBH và tứ giác BDCH là hình thoi
c, Tính diện tích hình thoi BDCH theo R trong trường hợp tam giác ABC đều
giúp vs ạ
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.Chứng minh tứ giác ANCE là hình thoi.c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG CG’.d) Cho AB 6cm, AC 8cm. Tính diện tích ΔDGG’.
Đọc tiếp
Cho tam giác ABC vuông tại A. Gọi M, N lần lượt là trung điểm của hai cạnh AB và BC.
a) Gọi D là điểm đối cứng của A qua N. Chứng minh tứ giác ABCD là hình chữ nhật.
b) Lấy I là trung điểm của cạnh AC và E là điểm đối xứng của N qua I.
Chứng minh tứ giác ANCE là hình thoi.
c) Đường thẳng BC cắt DM và DI lần lượt tại G và G’. Chứng minh BG = CG’.
d) Cho AB = 6cm, AC = 8cm. Tính diện tích ΔDGG’.
a) Ta có: NB = NC (gt); ND = NA (gt)
⇒ Tứ giác ABDC là hình bình hành
có ∠A = 90o (gt) ⇒ ABDC là hình chữ nhật.
b) Ta có: AI = IC (gt); NI = IE (gt)
⇒ AECN là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).
mặt khác ΔABC vuông có AN là trung tuyến nên AN = NC = BC/2.
Vậy tứ giác AECN là hình thoi.
c) BN và DM là 2 đường trung tuyến của tam giác ABD; BN và MD giao nhau tại G nên G là trọng tâm tam giác ABD.
Tương tự G’ là trọng tâm của hai tam giác ACD
⇒ BG = BN/3 và CG’ = CN/3 mà BN = CN (gt) ⇒ BG = CG’
d) Ta có: SABC = (1/2).AB.AC = (1/2).6.6 = 24 (cm2)
Lại có: BG = GG’ = CG’ (tính chất trọng tâm)
⇒ SDGB = SDGG' = SDG'C = 1/3 SBCD
(chung đường cao kẻ từ D và đáy bằng nhau)
Mà SBCD = SCBA (vì ΔBCD = ΔCBA (c.c.c))
⇒SDGG' = 24/3 = 8(cm2)
Đúng 1
Bình luận (2)
Bài tập : Cho tam giác ABC cân tại A và AM là trung tuyến .Gọi P,Q lần lượt là trung điểm của các cạnh AB,AC
a,Chứng minh Tứ giác APMQ là hình thoi
b,Lấy K đối xứng M qua Q.Tứ giác AMCK là hình gì?Vì sao
c,Tìm điều kiện của tam giác ABC để tứ giác AMCK là hình vuông
Xem chi tiết
Cho tam giác ABC vuông tại A (AB<AC) . Đường trung tuyến AM . Gọi I là trung điểm của AB và D là điểm đối xứng với M qua I a, Tính diện tích tam giác ABC biết AB=3cm, AC= 4cm b, Chứng minh tứ giác DAMB là hình thoi c, Chứng minh tứ giác DACM là hình bình hành d, Tìm điều kiện của tam giác ABC để tứ giác ADBM là hình vuông
Cho tam giác abc cân tại A có AH là đường cao. Gọi M và N lần lượt là trung điểm của AB và AC. Biết AH6cm, BC8cm.a)Tính diện tích tam giác ABC và độ dài cạnh MN.b) Gọi D là điểm đối xứng của H qua D. Chứng minh tứ giác AHBD là hình chữ nhật.c) Gọi E là điểm đối xứng của A qua H. Chứng minh tứ giác ABEC là hình thoi.d) Gọi F là hình chiếu của H lên cạnh BC, gọi I, K lần lượt là trung điểm của HF và CF. Chứng minh EI vuông góc với BF.
Đọc tiếp
Cho tam giác abc cân tại A có AH là đường cao. Gọi M và N lần lượt là trung điểm của AB và AC. Biết AH=6cm, BC=8cm.
a)Tính diện tích tam giác ABC và độ dài cạnh MN.
b) Gọi D là điểm đối xứng của H qua D. Chứng minh tứ giác AHBD là hình chữ nhật.
c) Gọi E là điểm đối xứng của A qua H. Chứng minh tứ giác ABEC là hình thoi.
d) Gọi F là hình chiếu của H lên cạnh BC, gọi I, K lần lượt là trung điểm của HF và CF. Chứng minh EI vuông góc với BF.
Cho Tam giác ABC cân tại A có AH là đường cao. Gọi M,N lần lượt là trung điểm AB và AC. Gọi K là điểm đối xứng của H qua M a) chứng minh AHBK là hình chữ nhật b) Tứ giác AKHC là hình gì? Vì sao c) Chứng minh AMHN là hình thoi d) tính diện tích Tam giác ABC biết AH=4cm, BC=8cm
a: Xét tứ giác AHBK có
M là trung điểm của AB
M là trung điểm của HK
Do đó: AHBK là hình bình hành
mà \(\widehat{AHB}=90^0\)
nên AHBK là hình chữ nhật
b:
Xét tứ giác AKHC có
AK//HC
AK=HC
Do đó: AKHC là hình bình hành
c: Xét ΔABC có
N là trung điểm của AC
H là trung điểm của BC
Do đó: NH là đường trung bình
=>NH//AB và NH=AB/2
hay NH//AM và NH=AM
=>AMHN là hình bình hành
mà AM=AN
nên AMHN là hình thoi
Đúng 1
Bình luận (0)
Câu 1 Cho tứ giác ABCD Gọi Q là trung điểm của AC đường thẳng qua Q cắt AB AC lần lượt tại I và K chứng minh diện tích tam giác AIK bằng diện tích tam giác CIKCâu 2 Cho tam giác ABC cân tại A Gọi M và N lần lượt là trung điểm của AB và AC .a) chứng minh tứ giác BMNC là hình thang .b). Trên tia đối của tia MN xác định điểm E sao cho NENM hỏi tứ giác AECM là hình gì vì saoCâu 3 Cho tam giác abc vuông tại a gọi D E theo thứ tự là trung điểm của AB BC Tính de biết BC 10 cm AB 8 cmCâu 4 cho tứ giá...
Đọc tiếp
Câu 1 Cho tứ giác ABCD Gọi Q là trung điểm của AC đường thẳng qua Q cắt AB AC lần lượt tại I và K chứng minh diện tích tam giác AIK bằng diện tích tam giác CIK
Câu 2 Cho tam giác ABC cân tại A Gọi M và N lần lượt là trung điểm của AB và AC .a) chứng minh tứ giác BMNC là hình thang .b). Trên tia đối của tia MN xác định điểm E sao cho NE=NM hỏi tứ giác AECM là hình gì vì sao
Câu 3 Cho tam giác abc vuông tại a gọi D E theo thứ tự là trung điểm của AB BC Tính de biết BC = 10 cm AB = 8 cm
Câu 4 cho tứ giác ABCD có Â = 90° B =60° C =120°. a)tính số đo góc D. b) tứ giác ABCD là hình gì vì sao?
Giúp mình với sắp thi rùi
Cho hình thoi ABCK gọi G,H,I,K lần lượt là trung điểm của các cạnh AB,BC,CD,DA
a Chứng minh tứ giác GHIK là hình chữ nhật
b Biết GH=10cm GK=7Cm tính diện tích tam giác GHK
a: Xét ΔABC có
G là trung điểm của AB
H là trung điểm của BC
Do đó: GH là đường trung bình
=>GH//AC và GH=AC/2(1)
Xét ΔADC có
K là trung điểm của AD
I là trung điểm của DC
Do đó: KI là đường trung bình
=>KI//AC và KI=AC/2(2)
Xét hình thang ABCD có
G là tđ của AB
I là tđ của CD
Do đó: GI là đường trung bình
=>GI=AD(3)
Xét hình thang ADCB có
K là tđ của AD
H là tđ của BC
Do đó: KH là đường trung bình
=>KH=AD/2(4)
Từ (1), (2), (3) và (4) suy ra GHIK là hình chữ nhật
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn và AB=AC. Đường tròn tâm O đường kính AB = 2R cắt BC, AC lần lượt tại I,K. Tiếp tuyến tại B của (O) cắt AI tại D, H là giao điểm của AI và BK
a) CM: Tứ giác IHKC nội tiếp
b) CM: BC là phân giác góc DBH và tứ giác BDCH là hình thoi
c) Tính diện tích BDCH theo R trong trường hợp tam giác ABC đều