 ai giúp em câu này với
ai giúp em câu này với
Em vẫn còn băn khoăn về câu này ấy ạ, nên ai đó giúp em câu này với em cảm ơn ạ.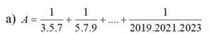
A = 1/3.5.7 + 1/5.7.9+ ... + 1/2019.2021.2023
2A = 2/3.5.7 + 2/5.7.9+ ... + 2/2019.2021.2023
2A = 1/3-1/5+1/7+1/5-1/7+1/9+....+1/2019-1/2021+1/2023
2A = 1/3 - 1/2023
2A = 2023/6069 - 3/6069
2A = 2023-3/6069
2A = 2020/6069
A = 1010/6069
Vậy A = 1010/6069
ai giúp em câu này với
\(A=\sqrt{\dfrac{3\sqrt{5}-1}{3+2\sqrt{5}}}-\sqrt{\dfrac{\sqrt{5}-1}{\sqrt{5}-2}}\)
\(=\sqrt{3-\sqrt{5}}-\sqrt{3+\sqrt{5}}\)
\(=\dfrac{\sqrt{5}-1-\sqrt{5}-1}{\sqrt{2}}\)
\(=-\sqrt{2}\)
Ai giúp em câu này với
Có ai giúp em câu này với em cảm ơn.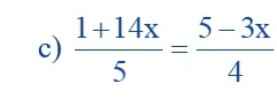
Lời giải:
$\frac{1+14x}{5}=\frac{5-3x}{4}$
$\Rightarrow 4(1+14x)=5(5-3x)$
$4+56x=25-15x$
$56x+15x=25-4$
$71x=21$
$x=\frac{21}{71}$
c, \(\Rightarrow4+56x=25-15x\Leftrightarrow71x=21\Leftrightarrow x=\dfrac{21}{71}\)

Có ai giúp em câu này với em cảm ơn.
số hs khá là: \(\dfrac{3}{4}\times\dfrac{1}{6}=\dfrac{1}{8}\left(hs\right)\)
a: số hs lớp 6A là : \(\dfrac{3}{4}+\dfrac{1}{8}+5=\dfrac{18}{24}+\dfrac{3}{24}+5=5\dfrac{21}{24}=5\dfrac{7}{8}=\dfrac{47}{8}\left(hs\right)\)
b: tỉ số là : \(\dfrac{3}{4}\times100:\dfrac{1}{8}=\dfrac{300}{4}:\dfrac{1}{8}=\dfrac{300\times8}{4\times1}=600\%\)
Gọi học sinh lớp 6a là x hs
Số học sinh giỏi là : \(\dfrac{3}{4}x\)(hs)
Số học sinh khác là : \(\dfrac{1}{6}.\dfrac{3}{4}x=\dfrac{1}{8}x\) (hs)
Theo bài ra có :
\(x-\dfrac{3}{4}x-\dfrac{1}{8}x=5\)
\(x\left(1-\dfrac{3}{4}-\dfrac{1}{8}\right)=5\)
\(\dfrac{1}{8}x=5\)
\(x=40\)
Vậy số hcj sinh lớp 6a là 40 hs
Số học sinh giỏi là : \(\dfrac{3}{4}.40=30\) (hs)
Số học sinh khá là :\(\dfrac{1}{6}.30=5\) (hs)
ĐS ...
Ai giúp em câu này với em cảm ơn nhiều.
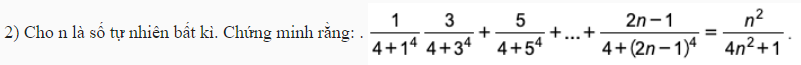
Chắc đề đúng là \(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...\)
- Với \(n=1\) đẳng thức đúng
- Giả sử đẳng thức cũng đúng với \(n=k>1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}=\dfrac{k^2}{4k^2+1}\)
- Ta cần chứng minh nó cũng đúng với \(n=k+1\) hay:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\)
Thật vậy, ta có:
\(\dfrac{1}{4+1^4}+\dfrac{3}{4+3^4}+...+\dfrac{2k-1}{4+\left(2k-1\right)^4}+\dfrac{2k+1}{4+\left(2k+1\right)^4}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{4+\left(2k+1\right)^4}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(2k+1\right)^4+4\left(2k+1\right)^2+4-4\left(2k+1\right)^2}=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+4k+3\right)^2-\left(4k+2\right)^2}\)
\(=\dfrac{k^2}{4k^2+1}+\dfrac{2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{k^2\left(4k^2+8k+5\right)+2k+1}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}\)
\(=\dfrac{\left(k+1\right)^2\left(4k^2+1\right)}{\left(4k^2+1\right)\left(4k^2+8k+5\right)}=\dfrac{\left(k+1\right)^2}{4k^2+8k+5}=\dfrac{\left(k+1\right)^2}{4\left(k+1\right)^2+1}\) (đpcm)
Ai giúp em câu này với ạ :((
\(=\left(6\sqrt{2}-6\sqrt{2}+6\sqrt{2}\right):\sqrt{2}=6\sqrt{2}:\sqrt{2}=6\)
\(=\left(6\sqrt{2}-6\sqrt{2}+6\sqrt{2}\right):\sqrt{2}=6\sqrt{2}:\sqrt{2}=6\)
Có ai giúp em câu này với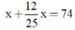
\(x+\dfrac{12}{25}x=74\\ \Rightarrow\left(1+\dfrac{12}{25}\right)x=74\\ \Rightarrow\dfrac{37}{25}x=74\\ \Rightarrow x=50\)
Ai giúp em câu này với ạ :((
\(lim_{n\rightarrow+\infty}\dfrac{6^n+1}{6^n-2}=\)\(lim_{n\rightarrow+\infty}\dfrac{6^n\left(1+\dfrac{1}{6^n}\right)}{6^n\left(1-\dfrac{2}{6^n}\right)}=\)\(lim_{n\rightarrow+\infty}\dfrac{\left(1+\dfrac{1}{6^n}\right)}{\left(1-\dfrac{2}{6^n}\right)}=\dfrac{1}{1}=1\)
\(lim_{n\rightarrow-\infty}\dfrac{6^n+1}{6^n-2}=\)\(\dfrac{0+1}{0-2}=\dfrac{-1}{2}\)