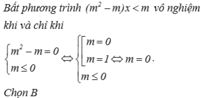Tìm tất cả các giá trị tham số mđể bất phương trình \(mx^2-2mx-1\ge0\) vô nghiệm.

Những câu hỏi liên quan
Câu 1: tìm tất cả các giá trị thực của tham số m để bất phương trình mx bình phương + 2mx -3
Xem chi tiết
Tìm tất cả các giá trị thực của tham số m để phương trình
2
(
x
2
+
m
x
)
-
2
(
2
x
2
+
2
m
x
+
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để phương trình 2 ( x 2 + m x ) - 2 ( 2 x 2 + 2 m x + m ) = x 2 +mx+m có nghiệm thực
A. ( - ∞ ; 0 ] ∪ [ 1 ; + ∞ ) .
B. ( - ∞ ; 0 ] ∪ [ 4 ; + ∞ ) .
C. ( - ∞ ; - 1 ] ∪ [ 0 ; + ∞ ) .
D. ( - ∞ ; - 4 ] ∪ [ 0 ; + ∞ ) .
Tìm tập tất các giá trị của tham số m để bất phương trình m 2 - m x < m vô nghiệm.
A. 0 ; 1
B. {0}
C. {0;1}
D. {1}
Bất phương trình ( m 2 - m ) x < m vô nghiệm khi và chỉ khi m 2 - m = 0 m ≤ 0 ⇔ [ m = 0 m = 1 ⇔ m = 0 m ≤ 0
Đúng 0
Bình luận (0)
Tìm tập tất các giá trị của tham số m để bất phương trình
m
2
-
m
x
m
vô nghiệm. A.
0
;
1
B.
0
C.
0
;
1
D.
1
Đọc tiếp
Tìm tập tất các giá trị của tham số m để bất phương trình m 2 - m x < m vô nghiệm.
A. 0 ; 1
B. 0
C. 0 ; 1
D. 1
Bài 1. Tìm m để f (x)=mx^2 -2(m-1)x+4m-1 luôn dương Bài 2 tìm tất cả các giá trị của tham số m để bất phương trình sau có nghiệm đúng với mọi a.5x^2-x+m>0 b.m(m+2)x^2+2mx+2>0
1) Tìm tập nghiệm S của bất phương trình | 2x+1| > x+1
2) Tìm tất cả giá trị của tham số m để bất phương trình -x^2+x-m>0 vô nghiệm
2: \(\text{Δ}=1^2-4\cdot\left(-1\right)\cdot\left(-m\right)=1-4m\)
Để bất phương trình vô nghiệm thì \(\left\{{}\begin{matrix}1-4m< 0\\-1< 0\end{matrix}\right.\Leftrightarrow m>\dfrac{1}{4}\)
Đúng 2
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình
x
-
3
0
m
-
x
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để hệ bất phương trình x - 3 < 0 m - x < 1 vô nghiệm.
A. m < 4
B. m > 4
C. m ≤ 4
D. m ≥ 4
Chọn D
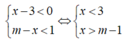
Hệ bất phương trình vô nghiệm khi và chỉ khi m - 1 ≥ 3 hay m ≥ 4
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để bất phương trình : -x2+x-m>0 vô nghiệm
BPT đã cho vô nghiệm khi:
\(-x^2+x-m\le0\) nghiệm đúng với mọi x
\(\Leftrightarrow\Delta'=1-4m\le0\)
\(\Rightarrow m\ge\dfrac{1}{4}\)
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình
3
x
-
1
+
m
x
+
1
2
x
2
-
1
4
có hai nghiệm thực? A.
1
3
≤
m...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho bất phương trình 3 x - 1 + m x + 1 = 2 x 2 - 1 4 có hai nghiệm thực?
A. 1 3 ≤ m < 1 .
B. - 1 ≤ m ≤ 1 4 .
C. - 2 < m ≤ 1 3 .
D. 0 ≤ m < 1 3 .