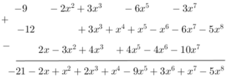\(1,=4x^2-2x+18x-9=2x\left(x-2\right)+9\left(x-2\right)=\left(2x+9\right)\left(x-2\right)\\ 2,=6x^2+3x+4x+2=3x\left(2x+1\right)+2\left(2x+1\right)=\left(3x+2\right)\left(2x+1\right)\\ 3,=-\left(5x^2+4x+25x+20\right)=-\left[x\left(5x+4\right)+5\left(5x+4\right)\right]=-\left(x+5\right)\left(5x+4\right)\\ 4,=-\left(7x^2-14x+3x-6\right)=-\left[7x\left(x-2\right)+3\left(x-2\right)\right]=-\left(7x+3\right)\left(x-2\right)\\ =\left(7x+3\right)\left(2-x\right)\)

\(x^3-4x^2+8x-8\)

\(=x^3-2x^2+4x-2x^2+4x-8\)

\(=\left(x^3-2x^2+4x\right)-\left(2x^2-4x+8\right)\)

\(=x\left(x^2-2x+4\right)-2\left(x^2-2x+4\right)\)

\(=\left(x^2-2x+4\right)\left(x-2\right)\)

a: \(=x\left(x^2+4x+4-z^2\right)\)

\(=x\left(x+2-z\right)\left(x+2+z\right)\)

10: \(x\left(x-y\right)+x^2-y^2\)

\(=x\left(x-y\right)+\left(x-y\right)\left(x+y\right)\)

\(=\left(x-y\right)\left(x+x+y\right)\)

\(=\left(x-y\right)\left(2x+y\right)\)

11: \(x^2-y^2+10x-10y\)

\(=\left(x^2-y^2\right)+\left(10x-10y\right)\)
\(=\left(x-y\right)\left(x+y\right)+10\left(x-y\right)\)

\(=\left(x-y\right)\left(x+y+10\right)\)

12: \(x^2-y^2+20x+20y\)

\(=\left(x^2-y^2\right)+\left(20x+20y\right)\)

\(=\left(x-y\right)\left(x+y\right)+20\left(x+y\right)\)

\(=\left(x+y\right)\left(x-y+20\right)\)

13: \(4x^2-9y^2-4x-6y\)

\(=\left(4x^2-9y^2\right)-\left(4x+6y\right)\)

\(=\left(2x-3y\right)\left(2x+3y\right)-2\left(2x+3y\right)\)

\(=\left(2x+3y\right)\left(2x-3y-2\right)\)

14: \(x^3-y^3+7x^2-7y^2\)

\(=\left(x^3-y^3\right)+\left(7x^2-7y^2\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\cdot\left(x^2-y^2\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2\right)+7\left(x-y\right)\left(x+y\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2+7x+7y\right)\)

15: \(x^3+4x-\left(y^3+4y\right)\)

\(=x^3-y^3+4x-4y\)

\(=\left(x^3-y^3\right)+\left(4x-4y\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2\right)+4\left(x-y\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2+4\right)\)

16: \(x^3+y^3+2x+2y\)

\(=\left(x^3+y^3\right)+\left(2x+2y\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2\right)+2\left(x+y\right)\)

\(=\left(x+y\right)\left(x^2-xy+y^2+2\right)\)

17: \(x^3-y^3-2x^2y+2xy^2\)

\(=\left(x^3-y^3\right)-\left(2x^2y-2xy^2\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2\right)-2xy\left(x-y\right)\)

\(=\left(x-y\right)\left(x^2+xy+y^2-2xy\right)\)

\(=\left(x-y\right)\left(x^2-xy+y^2\right)\)

18: \(x^3-4x^2+4x-xy^2\)

\(=x\left(x^2-4x+4-y^2\right)\)

\(=x\left[\left(x^2-4x+4\right)-y^2\right]\)

\(=x\left[\left(x-2\right)^2-y^2\right]\)

\(=x\left(x-2-y\right)\left(x-2+y\right)\)

Phân tích đa thức thành nhân tử nha

Đề sai rồi bạn

c: \(x^4+x^3-4x^2+x+1\)

\(=x^4-x^3+2x^3-2x^2-2x^2+2x-x+1\)

\(=\left(x-1\right)\left(x^3+2x^2-2x-1\right)\)

\(=\left(x-1\right)\left[\left(x-1\right)\left(x^2+x+1\right)+2x\left(x-1\right)\right]\)

\(=\left(x-1\right)^2\cdot\left(x^2+3x+1\right)\)

\(a,\Leftrightarrow x\left(2x-7\right)+2\left(2x-7\right)=0\\ \Leftrightarrow\left(x+2\right)\left(2x-7\right)=0\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=\dfrac{7}{2}\end{matrix}\right.\\ b,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ c,\Leftrightarrow\left(2x-1\right)\left(2x+1\right)-2\left(2x-1\right)^2=0\\ \Leftrightarrow\left(2x-1\right)\left(2x+1-4x+2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(-2x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\dfrac{3}{2}\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-1\right)-4\left(x-1\right)^2=0\\ \Leftrightarrow\left(x-1\right)\left(x^2-4x+4\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x-2\right)^2=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

* f(x) = x2 + 2x3− 7x5 − 9 − 6x7 + x3 + x2 + x5 − 4x2 + 3x7

= (x2+ x2 – 4x2)+ (2x3 + x3 ) - (7x5 - x5 ) – 9 – (6x7 – 3x7)

= - 2x2 + 3x3 – 6x5 – 9 – 3x7

Sắp xếp theo thứ tự tăng của biến: f(x) = −9 − 2x2 + 3x3 − 6x5 − 3x7

* g(x) = x5 + 2x3 − 5x8 − x7 + x3 + 4x2 -5x7 + x4 − 4x2 − x6 – 12

= x5+ (2x3 + x3) - 5x8 – (x7+ 5x7) + (4x2 – 4x2 ) + x4 – x6 – 12

= x5 + 3x3 – 5x8 – 6x7 + x4 – x6 – 12

Sắp xếp theo thứ tự tăng của biến: g(x) = −12 + 3x3 + x4 + x5 – x6 − 6x7− 5x8

* h(x) = x + 4x5 − 5x6 − x7 + 4x3 + x2 − 2x7 + x6 − 4x2 − 7x7 + x.

= (x+ x) +4x5 – (5x6 – x6)- (x7 + 2x7+ 7x7) + 4x3+ (x2 – 4x2)

= 2x + 4x5 - 4x6 – 10x7 + 4x3 -3x2

Sắp xếp theo thứ tự tăng của biến: h(x) = 2x − 3x2 + 4x3 + 4x5 − 4x6 − 10x7