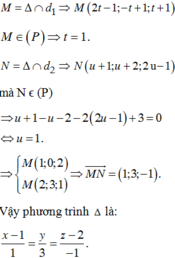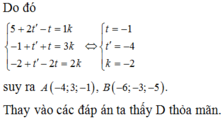Trong mặt phẳng với hệ tọa độ Oxy, cho hai đường thẳng d1 : 3x – y – 5 = 0, d2 :x-4=0. Viết phương trình đường tròn có bán kính R =5, tâm thuộc đường thẳng d1 với tung độ âm và cắt đường thẳng d2 theo dây cung có độ dài bằng 8.

Những câu hỏi liên quan
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
2
t
y
t
z
4
và
d...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x = 2 t y = t z = 4 và d 2 : x = 3 − t ' y = t ' z = 0 . Viết phương trình mặt cầu (S) có bán kính nhỏ nhất tiếp xúc với cả hai đường thẳng d 1 và d 2 .
A. S : x + 2 2 + y + 1 2 + z + 2 2 = 4.
B. S : x − 2 2 + y − 1 2 + z − 2 2 = 16.
C. S : x − 2 2 + y − 1 2 + z − 2 2 = 4.
D. S : x + 2 2 + y + 1 2 + z + 2 2 = 16.
Đáp án C
Gọi tâm mặt cầu cần tìm là I và H,K lần lượt là hình chiếu của I lên các đường thẳng d 1 , d 2 .
Ta có: I H + I K ≥ H K ≥ a d 1 , d 2 . Dấu bằng khi HK là đường vuông góc chung của d 1 , d 2 và I là trung điểm của HK.
Khi đó: H 2 a , a , 4 và K 3 − b , b , 0 ⇒ K H ¯ 2 a + b − 3 ; a − b ; 4
Đường thẳng d 1 , d 2 có vecto chỉ phương lần lượt là u 1 ¯ = 2 ; 1 ; 0 và u 2 ¯ − 1 ; 1 ; 0 nên:
K H ¯ . u 1 ¯ = 0 K H ¯ . u 2 ¯ = 0 ⇔ 2 2 a + b − 3 + a − b + 0.4 = 0 − 2 a + b − 3 + a − b + 0.4 = 0 ⇔ 2 a + b − 3 = a − b = 0 ⇔ a = b = 1
Suy ra trung điểm của HK là I 2 ; 1 ; 2 và bán kính của mặt cầu (S) là R = H K 2 = 2.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
+
1
2
y
-
1
-
1
z
-
1
1
;
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x + 1 2 = y - 1 - 1 = z - 1 1 ; d 2 = x - 1 1 = y - 2 1 = z + 1 2 và mặt phẳng (P): x-y-2z+3=0 Biết rằng đường thẳng ∆ nằm trên mặt phẳng (P) và cắt cả hai đường thẳng d 1 , d 2 Viết phương trình đường thẳng ∆
A. ∆ : x - 1 - 1 = y 3 = z - 2 1
B. ∆ : x - 2 1 = y - 3 3 = z - 1 1
C. ∆ : x - 2 1 = y - 3 - 3 = z - 1 1
D. ∆ : x - 1 1 = y 3 = z - 2 - 1
trong mặt phẳng tọa độ Oxy,cho hai đường thẳng d1:2x-y+5=0,d2:3x+6y-1=0 và điểm P(-2,0).Gọi A là giao điểm của d1 và d2.Khi đó đường thẳng d đi qua P và cùng với d1,d2 tạo thành một tam giác cân đỉnh A có phương trình là?
Gọi \(M\left(x;y\right)\) là điểm cách đều \(d_1\) và \(d_2\)
\(\Rightarrow\dfrac{\left|2x-y+5\right|}{\sqrt{2^2+\left(-1\right)^2}}=\dfrac{\left|3x+6y-1\right|}{\sqrt{3^2+6^2}}\)
\(\Leftrightarrow\left|6x-3y+15\right|=\left|3x+6y-1\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-9y+16=0\\9x+3y+14=0\end{matrix}\right.\)
\(\Rightarrow\) Phương trình đường thẳng cần tìm có dạng:
\(\left[{}\begin{matrix}9\left(x+2\right)+3\left(y-0\right)=0\\3\left(x+2\right)-9\left(y-0\right)=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+y+6=0\\x-3y+2=0\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn
Đúng 1
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-40 và hai đường thẳng
d
1
:
x
-
3
2
y
-
2
1
z
-
6
5
;
d
2
:...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-4=0 và hai đường thẳng d 1 : x - 3 2 = y - 2 1 = z - 6 5 ; d 2 : x - 6 3 = y 2 = z - 1 1 . Phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt hai đường thẳng d 1 , d 2 là:
A. x - 1 - 1 = y - 1 2 = z - 1 - 3
B. x - 1 2 = y - 1 - 3 = z - 1 - 1
C. x - 1 - 3 = y - 1 2 = z - 1 - 1
D. x - 1 2 = y - 1 - 1 = z - 1 - 3
Chọn B
Gọi A, B lần lượt là giao điểm của d1d2 với mặt phẳng (P). Đường thẳng d cần tìm đi qua A và B.
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-40 và hai đường thẳng
d
1
:
x
-
3
2
y
-
2
1
z
-
6...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho mặt phẳng (P): 2x+y+z-4=0 và hai đường thẳng d 1 : x - 3 2 = y - 2 1 = z - 6 5 , d 2 : x - 6 3 = y 2 = z - 1 1 . Phương trình đường thẳng d nằm trong mặt phẳng (P) và cắt hai đường thẳng d1, d2 là:
![]()
![]()
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và
d...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x+2y+3z-5=0. Đường thẳng Δ vuông góc với (P) cắt d1 và d2 có phương trình là:
![]()
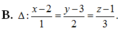
![]()
![]()
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
-
3
-
1
y
-
3
-
2
z
+
2
1
và...
Đọc tiếp
Trong không gian với hệ trục tọa độ Oxyz, cho hai đường thẳng d 1 : x - 3 - 1 = y - 3 - 2 = z + 2 1 và d 2 : x - 5 - 3 = y + 1 2 = z - 2 1 và mặt phẳng (P) có phương trình x + 2 y + 3 z - 5 = 0 . Đường thẳng Δ vuông góc với (P) cắt d 1 và d 2 có phương trình là:
A. ∆ : x - 1 1 = y + 1 2 = z 3
B. ∆ : x - 2 1 = y - 3 2 = z - 1 3
C. ∆ : x - 3 1 = y - 3 2 = z + 2 3
C. ∆ : x - 1 3 = y + 1 2 = z 1
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
+
3
1
y
-
2
-
1
z
-
1
2
,
d
2
:...
Đọc tiếp
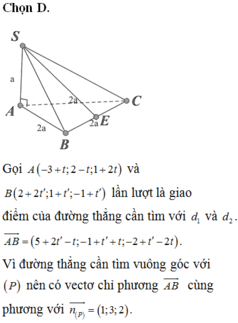
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x + 3 1 = y - 2 - 1 = z - 1 2 , d 2 : x - 2 2 = y - 1 1 = z + 1 1 và mặt phẳng P : x + 3 y + 2 z - 5 = 0 Đường thẳng vuông góc với (P), cắt cả d 1 và d 2 có phương trình là:
A. x + 7 1 = y - 6 3 = z + 7 2
B. x + 3 1 = y + 2 3 = z - 1 2
C. x 1 = y 3 = z + 2 2 .
D. x + 4 1 = y - 3 3 = z + 1 2
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng
d
1
:
x
+
3
1
y
-
2
-
1
z
-
1
2
,
d
2...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, cho hai đường thẳng d 1 : x + 3 1 = y - 2 - 1 = z - 1 2 , d 2 : x - 2 2 = y - 1 1 = z + 1 1 , và mặt phẳng (P):x+3y+2z-5=0. Đường thẳng vuông góc với (P), cắt cả d 1 và d 2 có phương trình là:
![]()
![]()
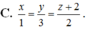
![]()