Xét ΔAMN và ΔABC có

góc AMN=góc ABC

góc A chung

=>ΔAMN đồng dạng với ΔABC

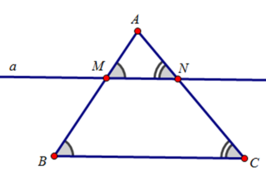
 Hai tam giác AMN và ABC có các góc tương ứng bằng nhau:

∠A = ∠A ;

∠M = ∠B; ( hai góc đồng vị)

∠N = ∠C; ( hai góc đồng vị)

- Và có các cạnh tương ứng tỉ lệ với nhau

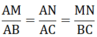
( theo hệ quả định lí ta- let)

MK chỉ cần câu d thôi 

,,

Giải hộ mình câu cuối phần d nha, 😊

a, xét tam giác AMB và tam giác AMC có :

AB=AC (gt)

MB=MC (gt)

AM là cạnh chung

suy ra: tam giác AMB = tam giác AMC (c.c.c)

b,Vì tam giác AMB = tam giác AMC ( câu a)

suy ra : góc B =góc C ( 2 góc tương ứng )

xét tam giác MBE và tam giác MCF có:

M1=M2 ( đối đỉnh )

B =C

MB=MC ( gt)

suy ra :tam giác MBE = tam giác MCF (g.c.g)

vì tam giác MBE = tam giác MCF (chứng minh trên)

ME=MF (2 cạch tương ứng )

xét tam giác AEM và tam giác AFM có :

E1=F1

AM là cạnh chung

ME=MF

suy ra : tam giác AEM = tam giác AFM (c.g.c)

vì tam giác AEM = tam giác AFM ( chứng minh trên)

suy ra :AE=AF

c, gọi điểm cắt nhau của EF và AM 

Vì tam giác AMB = tam giác AMC (câu b)

suy ra : góc A1 = góc A2 ( 2 góc tương ứng ); góc M1 = góc M2 ( 2 góc tương ứng)

xét tam giác AEH và tam giác AFH có :

A1=A2 

AE=AF

AH là điểm chung 

suy ra : tam giác AEH = tam giác AFH (c.g.c)

suy ra góc H1= góc H2 ( 2 góc tương ứng)

mà H1+H2=180 (2 góc kề bù)

suy ra : H1=H2=90

suy ra AM vuông góc với EF

mà M1+M2=180

suy ra M1=M2=90

suy ra AM vuông góc với BC

     mà AM vuông góc với EF

suy ra EF song song với BC ( 2 đường thẳng phân biệt cùng vuông góc với đường thẳng thứ 3 thì chúng song song với nhau )

d, Ta có : AMB = NMC ( đối đỉnh )

+) AMB+AMC= 180 ( 2 góc kề bù )

mà AMC=NMC 

suy ra AMB+NMC =180 (3)

mà     AMB+NMC = AMN (4)

Từ (3),(4) suy ra : 3 điểm A,M,N thẳng hàng 

1, xét tam giác AMB và tam giác AMC có:

AB=AC (gt)

MB=MC (gt)

1: Xét tứ giác ADHE có

\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)

=>ADHE là hình chữ nhật

=>AH=DE

2: \(\widehat{EDM}=90^0\)

=>\(\widehat{EDH}+\widehat{MDH}=90^0\)

=>\(\widehat{EAH}+\widehat{MDH}=90^0\)

=>\(\widehat{MDH}+\widehat{HAC}=90^0\)

=>\(\widehat{MDH}+\widehat{ABC}=90^0\)

mà \(\widehat{MHD}+\widehat{MBD}=90^0\)

nên \(\widehat{MDH}=\widehat{MHD}\)

=>MD=MH

\(\widehat{MDH}+\widehat{MDB}=\widehat{HDB}=90^0\)

\(\widehat{MHD}+\widehat{MBD}=90^0\)(ΔHDB vuông tại D)

mà \(\widehat{MDH}=\widehat{MHD}\)

nên \(\widehat{MDB}=\widehat{MBD}\)

=>MD=MB

=>MB=MH

=>M là trung điểm của BH

\(\widehat{NED}=90^0\)

=>\(\widehat{NEH}+\widehat{DEH}=90^0\)

=>\(\widehat{NEH}+\widehat{DAH}=90^0\)

mà \(\widehat{DAH}=\widehat{C}\left(=90^0-\widehat{ABC}\right)\)

nên \(\widehat{NEH}+\widehat{C}=90^0\)

mà \(\widehat{NHE}+\widehat{C}=90^0\)(ΔHEC vuông tại E)

nên \(\widehat{NEH}=\widehat{NHE}\)

=>NE=NH

\(\widehat{NEH}+\widehat{NEC}=\widehat{CEH}=90^0\)

\(\widehat{NHE}+\widehat{NCE}=90^0\)(ΔCEH vuông tại E)

mà \(\widehat{NHE}=\widehat{NEH}\)

nên \(\widehat{NEC}=\widehat{NCE}\)

=>NE=NC

mà NH=NE

nên NC=NH

=>N là trung điểm của HC