Giải bất phương trình sau :
2x^3 > x + 1
Giải phương trìnhsau x/2x-6-x/2x+2=2x/(x+1)(x-3) Giải bất phương trình sau 12x+1/12_< 9x+1/3 - 8x+1/4
\(\dfrac{x}{2x-6}-\dfrac{x}{2x+2}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\left(ĐKXĐ:x\ne-1,x\ne3\right)\)
\(\Leftrightarrow\dfrac{x}{2\left(x-3\right)}-\dfrac{x}{2\left(x+1\right)}=\dfrac{2x}{\left(x+1\right)\left(x-3\right)}\)
\(\Leftrightarrow\dfrac{x\left(x+1\right)}{2\left(x+1\right)\left(x-3\right)}-\dfrac{x\left(x-3\right)}{2\left(x+1\right)\left(x-3\right)}=\dfrac{2x\cdot2}{2\left(x+1\right)\left(x-3\right)}\)
\(\Rightarrow x\left(x+1\right)-x\left(x-3\right)=4x\)
\(\Leftrightarrow x^2+x-x^2+3x=4x\)
\(\Leftrightarrow x^2+x-x^2+3x-4x=0\)
\(\Leftrightarrow0x=0\)
Phương trình có vô số nghiệm , trừ x = -1,x = 3
Vậy ...
\(\dfrac{12x+1}{12}< \dfrac{9x+1}{3}-\dfrac{8x+1}{4}\)
\(\Leftrightarrow12\cdot\dfrac{12x+1}{12}< 12\cdot\dfrac{9x+1}{3}-12\cdot\dfrac{8x+1}{4}\)
\(\Leftrightarrow12x+1< 4\left(9x+1\right)-3\left(8x+1\right)\)
\(\Leftrightarrow12x+1< 36x+4-24x-3\)
\(\Leftrightarrow12x+1< 12x+1\)
\(\Leftrightarrow12x-12x< 1-1\)
\(\Leftrightarrow0x< 0\)
Vậy S = {x | x \(\in R\)}
Giải phương trình và bất phương trình sau:
a ) | 3 x | = x + 6 b ) x + 2 x - 2 - 1 x = 2 x x - 2 c ) ( x + 1 ) ( 2 x – 2 ) – 3 > – 5 x – ( 2 x + 1 ) ( 3 – x )
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
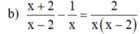
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
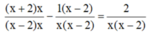
![]()
![]()
![]()
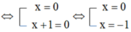
![]()
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
1) Giải các phương trình sau : a) x-3/x=2-x-3/x+3 b) 3x^2-2x-16=0 2) Giải bất phương trình sau: 4x-3/4>3x-5/3-2x-7/12
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
giải bất phương trình 2x-3/x-1<1/3
giải bất phương trình 2x-3/x-1 > 1/3
\(\dfrac{2x-3}{x-1}< \dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow6x-9< x-1\Leftrightarrow5x< 8\Leftrightarrow x< \dfrac{8}{5}\) và ĐK \(x\ne1\)
\(\dfrac{2x-3}{x-1}>\dfrac{1}{3}\left(đk:x\ne1\right)\)
\(\Leftrightarrow x-1< 6x-9\Leftrightarrow5x>8\Leftrightarrow x>\dfrac{8}{5}\) và ĐK \(x\ne1\)
Giải bất phương trình sau: (2x - 1)(x + 3) - 3x + 1 ≤ (x - 1)(x + 3) + x2 - 5
(2x – 1)(x + 3) – 3x + 1 ≤ (x – 1)(x + 3) + x2 – 5
⇔ 2x2 + 6x - x – 3 – 3x + 1 ≤ x2 + 3x - x – 3 + x2 – 5
⇔ 2x2 + 2x – 2 ≤ 2x2 + 2x – 8
⇔ 6 ≤ 0 (Vô lý).
Vậy BPT vô nghiệm.
Bài 1: Giải các bất phương trình và phương trình sau :
a) 2(3-4x) = 10-(2x – 5)
Giải các bất phương trình và phương trình sau :
a) 3(2-4x) = 11-(3x – 1)
Bài 1:
a) Ta có: \(2\left(3-4x\right)=10-\left(2x-5\right)\)
\(\Leftrightarrow6-8x-10+2x-5=0\)
\(\Leftrightarrow-6x+11=0\)
\(\Leftrightarrow-6x=-11\)
hay \(x=\dfrac{11}{6}\)
b) Ta có: \(3\left(2-4x\right)=11-\left(3x-1\right)\)
\(\Leftrightarrow6-12x-11+3x-1=0\)
\(\Leftrightarrow-9x-6=0\)
\(\Leftrightarrow-9x=6\)
hay \(x=-\dfrac{2}{3}\)
Giải bất phương trình sau x-3/5 +1 < 2x-5
`(x-3)/5+1<2x-5`
`<=>x-3+5<5(2x-5)`
`<=>x+2<10x-25`
`<=>8x>27`
`<=>x>27/8`
Vậy `S={x|x>27/8}`
Giải các bất phương trình sau:
a) 2 x − 5 = x + 3 ; b) 3 x − 1 − 2 = 2 x
Giải bất phương trình sau:
x^2-2x+3|x-1|<3
\(x^2-2x+3\left|x-1\right|< 3\)
\(-3< x-1< 3\)
\(-2< x< 4\)
\(x\in\left\{-1;0;1;2;3\right\}\)
Tìm sai lầm trong các "lời giải" sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình 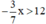 . Ta có:
. Ta có:
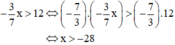
a) Sai lầm là coi -2 là hạng từ và chuyển vế hạng tử này trong khi -2 là một nhân tử.
Lời giải đúng:
-2x > 23
⇔ x < 23 : (-2) (chia cho số âm nên đổi chiều)
⇔ x < -11,5
Vậy nghiệm của bất phương trình là x < -11,5
b) Sai lầm là nhân hai vế của bất phương trình với 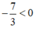 mà không đổi chiều bất phương trình.
mà không đổi chiều bất phương trình.
Lời giải đúng:
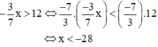
Vậy nghiệm của bất phương trình là x < -28