Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm M của mỗi đường (AB # CD)
a' Chứng minh AC=BD
b'Chứng minh AD=BC
Những câu hỏi liên quan
Bài 1: Hai đoạn thẳng AB và CD cắt nhau tại I và I là trung điểm của mỗi đoạn. Cho biết:
AB = 6cm, CD = 8cm,
0 AIC 60 .
a) Tìm độ dài hình chiếu của đoạn thẳng CD trên đường thẳng AB.
b) Tìm độ dài hình chiếu của đoạn thẳng AB trên đường thẳng CD.
Cho hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn thẳng. Gọi M và N lần lượt là trung điểm của AC và BD. CMR 3 điểm M,O,N thẳng hàng.
Bạn tham khảo https://h.vn/hoi-dap/question/147625.html nha
Đúng 0
Bình luận (0)
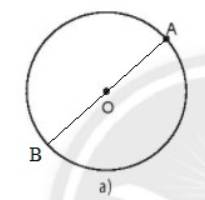
a) Lấy một điểm A bất kì trên đường tròn tâm O. Hãy tìm điểm B trên đường tròn sao cho O là trung điểm của đoạn thẳng AB (Hình 1a).
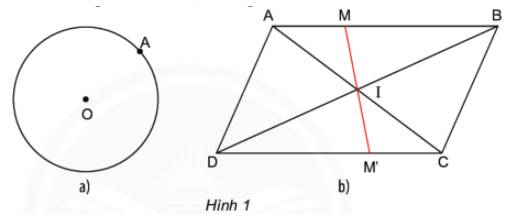
b) Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại I. Đường thẳng qua I cắt AB tại M và cắt CD tại M. Đo rồi so sánh độ dài IM và IM (Hình 1b).
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
b) Độ dài IM = IM'.
Đúng 0
Bình luận (0)
2 đoạn thẳng AB và CD cắt nhau tại I, I là trung điểm của mỗi đoạn thẳng. AB= 6cm, CD= 8cm, góc AIC= 60 độ
a, Tìm độ dài hình chiếu của đoạn thẳng AB trên đường thẳng CD
b, tìm độ dài hình chiếu của CD trên đường thẳng AB
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm của mỗi đoạn. Gọi E và F theo thứ tự là trung điểm của các đoạn thẳng AD và BD. Các đoạn thẳng CE và CF lần lượt cắt đoạn thẳng AB tại I, J. Chứng minh rằng: AI = IJ = JB
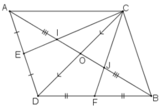
Gọi O là giao điểm của hai đoạn thẳng AB và CD.
⇒ AO = OB và CO = OD.
+ ΔACD có trung tuyến AO, CE cắt nhau tại I
⇒ I là trọng tâm ΔACD
⇒ AI = 2/3. AO = 2/3. 1/2. AB = 1/3.AB
+ Tương tự J là trọng tâm ΔBCD
⇒ BJ = 2/3. BO = 2/3. 1/2. BA = 1/3.AB
⇒ IJ = AB – AI – BJ = 1/3.AB
Vậy AI = IJ = JB
Đúng 0
Bình luận (0)
Hai đoạn thẳng AB và CD cắt nhau ở I, I là trung điểm của mỗi đoạn thẳng. Cho AB=6cm, CD=8cm, góc AIC=60 độ
a) Tìm độ dài hình chiếu của đoạn thẳng CD trên đường thẳng AB
b) Tìm độ dài hình chiếu của đoạn thẳng AB
trên đường thẳng CD
Bài 12. Cho hai đoạn thẳng AB, CD vuông góc với nhau và cắt nhau tại trung điểm của mỗi đoạn. Chứng minh rằng các đoạn thẳng AC, CB, BD, DA bằng nhau
Hai đoạn thẳng AB và CD cắt nhau tại trung điểm O của mỗi đoạn. Chứng minh rằng AC // BD
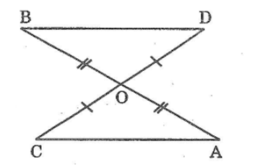
Xét Δ AOC và Δ BOD, ta có:
OA = OB ( Vì O là trung điểm của AB )
∠(AOC) =∠(BOD) (đối đỉnh)
OC = OD ( Vì O là trung điểm của CD)
Suy ra: ΔAOC = ΔBOD (c.g.c)
⇒∠A =∠B (hai góc tương ứng)
Vậy: AC // BD (vì có hai góc so le trong bằng nhau)
Đúng 0
Bình luận (0)
cho 2 đoạn thẳng AB và BD cắt nhau tại trung điểm O ở mỗi đoạn . m và n theo thứ tự là trung điểm của AB và CD . CMR :O là trung điểm của MN