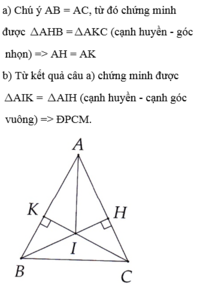
Cho tam giác ABC cân tại A, kẻ \(BH\perp AC\), CK\(\perp\)AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.

Những câu hỏi liên quan
Bài 5:Cho tam giác ABC cân tại A, kẻ BH ⊥ AC, CK ⊥ AB. Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc A.
Cho tam giác .ABC cân tại A. Kẻ BH | AC; CK perp AB ( H in AC ; K in AB ). a) Chứng minh tam giác AKH là tam giác cản b) Gọi I là giao của BH và CK; A cắt BC tại M. Chứng minh rằng IM là phân giác của hat BIC c) Chứng minh. HK //BC
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc HAB chung
=>ΔAHB=ΔAKC
=>AH=AK
b: Xét ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chung
góc KBC=góc HCB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC can tại I
Xét ΔABC có
BH,CK là đường cao
BH cắt CK tại I
=>I là trực tâm
=>AI vuông góc BC tại M
ΔIBC cân tại I
mà IM là đường cao
nên IM là phân giác của góc BIC
c: Xét ΔABC có AK/AB=AH/AC
nên KH//BC
Đúng 2
Bình luận (0)
Cho tam giác ABC cân tại A ( A ^ < 90 ° ) . Kẻ BH vuông góc với AC, CK vuông góc với AB ( H ∈ A C , K ∈ A B ) .
a) Chứng minh AH = AK
b) Gọi I là giao điểm của BH và CK. Chúng minh AI là tia phân giác của góc A.
Bài 3 (3,5 điểm): Cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC tại H, CK vuông góc với AB tại K.
a, Chứng minh AH = AK
b, Gọi I là giao điểm của BH và CK. Chứng minh AI là tia phân giác của góc BAC
c, Chứng minh tam giác BIC là tam giác cân
d, Chứng minh KH song song với BC
Cho tam giác ABC cân tại A . Kẻ BH ⊥ AC; CK ⊥ AB ( H ∈ AC; K ∈ AB ) a) Chứng minh tam giác AKH là tam giác cân. b) Gọi I là giao điểm của BH và CK; AI cắt BC tại M.Chứng minh rằng IM là phân giác của góc BIC. c) Chứng minh HK // BC
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
=>ΔAHB=ΔAKC
=>AH=AK
=>ΔAHK cân tại A
b: Xet ΔKBC vuông tại K và ΔHCB vuông tại H có
BC chug
KC=HB
=>ΔKBC=ΔHCB
=>góc IBC=góc ICB
=>ΔIBC cân tại I
mà IM vuông góc BC
nen IM là phân giác của góc BIC
c: Xét ΔABC có AK/AB=AH/AC
nên HK//BC
Đúng 0
Bình luận (0)
cho tam giác ABC cân tại A ( Â<90 độ). kẻ BH vuông góc với AC ( H thuộc AC) , CK vuông góc AB (K thuộc AB)
a) chứng minh: tam giác ABH= tam giác ACK
b)chứng minh : AH=AK
c) gọi I là giao điểm BH và CK. chứng minh AI là tia phân giác góc BAC
a: Xét ΔAHB vuông tại H và ΔAKC vuông tại K có
AB=AC
góc BAH chung
Do đó: ΔAHB=ΔAKC
b: ΔAHB=ΔAKC
=>AH=AK
c: Xét ΔAKI vuông tại K và ΔAHI vuông tại H co
AI chung
AH=AK
Do đó: ΔAKI=ΔAHI
=>góc KAI=góc HAI
=>AI là phân giác của góc BAC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A \(\left(\widehat{A}< 90^0\right)\). Vẽ \(BH\perp AC\left(H\in AC\right),CK\perp AB\left(K\in AB\right)\)
a) Chứng minh rằng AH = AK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là phân giác của góc A
a) Hai tam giác vuông ABH và ACK có:
AB = AC(gt)
Góc A chung.
nên ∆ABH = ∆ACK(Cạnh huyền- Góc nhọn)
suy ra AH = AK.
b) Hai tam giác vuông AIK và AIH có:
AK = AH(cmt)
AI cạnh chung
Nên ∆AIK = ∆AIH(cạnh huyền- cạnh góc vuông)
Suy ra ˆIAKIAK^=ˆIAHIAH^
Vậy AI là tia phân giác của góc A.
Đúng 0
Bình luận (0)
a) Hai tam giác vuông ABH và ACH có:
Tam giác ABC cân tại A ⇒ AB = AC
AH cạnh chung.
Nên ∆ABH = ∆ACH(Cạnh huyền – cạnh góc vuông)
Suy ra HB = HC
b)∆ABH = ∆ACH (Câu a)
Suy ra ∠BAH = ∠CAH (Hai góc tương ứng)
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC (H thuộc AC), kẻ CK vuông góc với AB (K thuộc BC).
a) Chứng minh AH = AK
b) Gọi I là giao điểm của BH và CK. Chứng minh rằng AI là tia phân giác của Â.
Toán lp 7 hả mk ko quen
Năm nay mk mới chỉ lên lớp 7 thôi
Năm nay mk mới được học kiến thức của lp 7 lên mk ko thể giải được bài toán này
Những xin bn Nguyễn Thị Thanh Hải hãy cho mk 1 L-I-K-E
hãy cho mk 1 L-I-K-E
~Chúc bn Nguyễn Thị Thanh Hải học giỏi~
Gặp nhiều may mắn trong cuộc sống
Đúng 2
Bình luận (0)
cho tam giác ABC cân tại A. Kẻ BH vuông góc với AC, CK vuông góc với AB: chứng minh:
a AH = AK, BH = CK
b gọi i là giao của BH và CK. c/m AI là là phân giác của A
Help