một viên đá được thả từ trên cao xuống đất sau t giây viên đá rơi được 2 m biết rằng h = 5 t mũ 2 tính quãng đường viên đá rơi được sau 1,5 giây

Những câu hỏi liên quan
một viên đá được thả từ trên cao xuống đất sau t giây viên đá rơi được 2 m biết rằng h = 5 t mũ 2 tính quãng đường viên đã rơi được sau 1,5 giây
Một viên đá được thả từ trên cao xuống đất. Sau t giây viên đá rơi được h (m). Biết rằng h = 5t2, tính quãng đường viên đá rơi được sau 1,5 giây.
Một viên đá được thả từ trên cao xuống đất. Sau t giây viên đá rơi được h(m). Biết rằng h=5t^2. Tính quãng đường viên đá rơi được sau1,5 giây.
Quãng đường viên đá rơi được sau 1,5s:
\(5.1,5^2=11,25\left(m\right)\)
Vậy...
Vì theo bài toán ta có t = 1,5 giây
\(\Rightarrow\)\(h=5t^2=5.\left(1,5\right)^2=\frac{45}{4}\)
Tính khoảng thời gian rơi tự do t của một viên đá. Cho biết trong giây cuối cùng trước khi chạm đất, vật đã rơi được đoạn đường dài 24,5 m. Lấy gia tốc rơi tự do g = 9,8 m/ s 2
Nếu gọi s là quãng đường viên đá đi được sau khoảng thời gian t kể từ khi bắt đầu rơi tới khi chạm đất và gọi s 1 là quãng đường viên đá đi được trước khi chạm đất 1 s, tức là sau khoảng thời gian t 1 = t -1 thì ta có các công thức
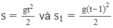
Từ đó suy ra quãng đường viên đá đi được trong 1 s cuối trước khi chạm đất là:
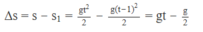
Với ∆ s = 24,5 m và g = 10 m/ s 2 , ta tìm được khoảng thời gian rơi tự do của viên đá
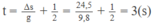
Đúng 1
Bình luận (0)
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bó...
Đọc tiếp
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (tính bằng giây ), kể từ khi quả bóng được đá lên; h là độ cao( tính bằng mét ) của quả bóng. Giả thiết rằng quả bóng được đá lên từ độ cao 1,2m. Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở độ cao 6m. Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo của quả bóng trong tình huống trên.
A. y = 4,9 t 2 + 12,2t + 1,2.
B. y = −4,9 t 2 + 12,2t + 1,2.
C. y = −4,9 t 2 + 12,2t − 1,2.
D. y = −4,9 t 2 − 12,2t + 1,2.
Một viên bi rơi tự do từ độ cao 19,6 m xuống mặt đất. Độ cao h (mét) so với mặt đất của viên bi trong khi rơi phụ thuộc vào thời gian t (giây) theo công thức: \(h = 19,6 - 4,9{t^2};h,t \ge 0\).
a) Hỏi sau bao nhiêu giây kể từ khi rơi viên bi chạm đất?
b) Tìm tập xác định và tập giá trị của hàm số h.
a) Để viên bi chạm đất thì \(\begin{array}{l}h = 0 \Leftrightarrow 19,6 - 4,9{t^2} = 0\\ \Leftrightarrow 4,9{t^2} = 19,6 \Leftrightarrow {t^2} = 4\end{array}\)
Do \(t \ge 0\) nên t=2(s)
Vậy sau 2 giây thì viên bi chạm đất
b) Theo bài ra ta có: \(t \ge 0\) nên tập xác định của hàm số h là \(D = \left[ {0; + \infty } \right)\)
Mặt khác: \(4,9{t^2} \ge 0 \Rightarrow 19,6 - 4,9{t^2} \le 19,6\)
\( \Rightarrow 0 \le h \le 19,6\). Do đó tập giá trị của hàm số h là \(\left[ {0;19,6} \right]\)
Đúng 0
Bình luận (0)
Chuyển động của vật nào dưới đây không thể coi là chuyển động rơi tự do ?A. Một viên đá nhỏ được thả rơi từ trên cao xuống đất.B. Các hạt mưa nhỏ lúc bắt đầu rơi.C. Một chiếc lá rụng đang rơi từ trên cây xuống đất.D. Một viên bi chì đang rơi ở trong ống thuỷ tinh đặt thẳng đứng và đã được hút chân không.
Đọc tiếp
Chuyển động của vật nào dưới đây không thể coi là chuyển động rơi tự do ?
A. Một viên đá nhỏ được thả rơi từ trên cao xuống đất.
B. Các hạt mưa nhỏ lúc bắt đầu rơi.
C. Một chiếc lá rụng đang rơi từ trên cây xuống đất.
D. Một viên bi chì đang rơi ở trong ống thuỷ tinh đặt thẳng đứng và đã được hút chân không.
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (giây) kể từ khi quả bóng được đá lên; h là độ cao (mét). Giả thiết quả bóng được đá từ độ cao 1m và đạt được độ cao 6m sau 1 giây đồng thời sau 6 giây quả bóng lại trở về độ cao 1m. Hỏi trong khoảng thời gian 5 giây, kể từ lúc bắt đầu được đá, độ cao lớn nhất của quả bóng đặt được bằng bao nhiêu? A. 9m B. 10m C. 6m...
Đọc tiếp
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth, trong đó t là thời gian (giây) kể từ khi quả bóng được đá lên; h là độ cao (mét). Giả thiết quả bóng được đá từ độ cao 1m và đạt được độ cao 6m sau 1 giây đồng thời sau 6 giây quả bóng lại trở về độ cao 1m. Hỏi trong khoảng thời gian 5 giây, kể từ lúc bắt đầu được đá, độ cao lớn nhất của quả bóng đặt được bằng bao nhiêu?
A. 9m
B. 10m
C. 6m
D. 13m
khi một quả bóng được đá lên , nó sẽ đạt tới độ cao nào đó rồi rơi xuống . Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth , trong đó t là hời gian ( tính bằng giây ) , kể từ khi quả bóng được đá lên ; h là độ cao ( tính bằng mét ) của quả bóng . Gỉa thiết rằng quả bóng được đá lên với độ cao 1,2 m . Sau đó một giây , nó đạt độ cao 8,5 m và sau 2 giây sau khi đá lên , nó ở độ cao 6 m : a) hãy tìm hàm số bậc 2 biểu thị độ cao h theo thời gian t và có phần đồ...
Đọc tiếp
khi một quả bóng được đá lên , nó sẽ đạt tới độ cao nào đó rồi rơi xuống . Biết rằng quỹ đạo của quả bóng là một cung parabol trong mặt phẳng với hệ tọa độ Oth , trong đó t là hời gian ( tính bằng giây ) , kể từ khi quả bóng được đá lên ; h là độ cao ( tính bằng mét ) của quả bóng . Gỉa thiết rằng quả bóng được đá lên với độ cao 1,2 m . Sau đó một giây , nó đạt độ cao 8,5 m và sau 2 giây sau khi đá lên , nó ở độ cao 6 m : a) hãy tìm hàm số bậc 2 biểu thị độ cao h theo thời gian t và có phần đồ thị trùng với quỹ đạo quả bóng trong tình huống trên ; b) xác định độ cao lớn nhất của quả bóng ( tính chính xác đến hàng phần nghìn); c) sau bao lâu thì quả bóng sẽ chạm đất kể từ khi đá lên ( tính chính xác đến hàng phần trăm) ?














