Biểu diễn ký tự c có số thứ tự 99 và kí tự m có số thứ tự 108 bằng dãy bít nhị phân.

Những câu hỏi liên quan
Xét dãy x1x2x3.....x10. Trong đó mỗi kí tự xi (1 <= i <= 10) chỉ nhận trong 2 giá trị 0 và 1. Dãy đó là dãy nhị phân 10bit.
a) Có bao nhiêu dãy nhị phân 10bit
b) Có bao nhiêu dãy nhị phân 10bit mà trong đó có ít nhất 3 kí tự 0 và ít nhất 3 kí tự 1.
c) Có bao nhiêu dãy nhị phân 10bit mà trong mỗi dãy chỉ có đúng 3 kí tự 0 và 3 kí tự 0 đó đứng liền nhau.
Viết các số tự nhiên có tổng các chữ số bằng 9 theo thứ tự tăng dần ta được dãy số:
9; 18; 27; 36; 45; 54; 63; 72; 81; 90; 108; 117; 126…
Hỏi số tự nhiên ở vị trí thứ 2017 của dãy số trên là số nào?
Giải
Số thứ 2017 là:
9+(2016*9)=18153.
ĐS:18153.
Ủng hộ mk nhá các bn
Đúng 0
Bình luận (0)
sai hết rồi , tổng các chữ số bằng chín mà số đó tổng bằng 27 òi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Theo em, với dãy đã sắp thứ tự và cho một số x cụ thể
a) Trường hợp nào tìm kiếm tuần tự nhanh hơn tìm kiếm nhị phân?
b) Về trung bình thuật toán tìm kiếm tuần tự hay thuật toán tìm kiếm nhị phân tốt hơn?
a. Ví dụ một bài toán tìm kiếm trong thực tế: Giáo viên muốn tìm tên bạn Chung trong danh sách lớp sau:

Các bước thực hiện thuật toán tìm kiếm nhị phân cho bài toán trên:
- Bước 1: Xét vị trí ở giữa dãy, đó là vị trí số 5
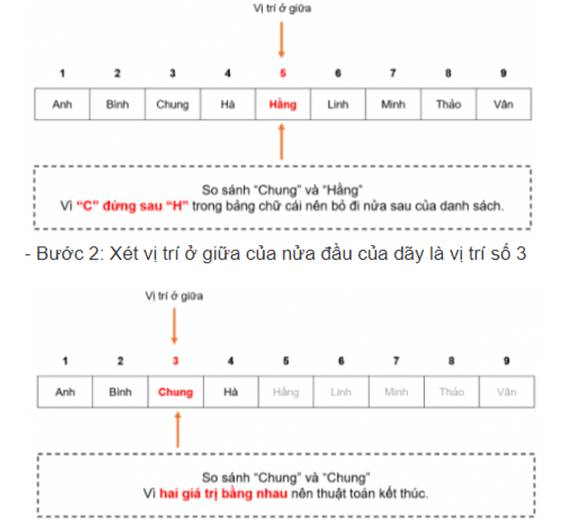
- Vì sau bước 2 đã tìm thấy tên học sinh nên thuật toán kết thúc.
b) Thuật toán tìm kiếm nhị phân
- Thuật toán tìm kiếm nhị phân thu hẹp được phạm vi tìm kiếm chỉ còn tối đa là một nửa sau mỗi lần lặp. Thuật toán chia bài toán thành những bài toán nhỏ hơn giúp tăng hiệu quả tìm kiếm.
Thuật toán tuần tự
- Mô tả thuật toán phải cụ thể, rõ ràng, đầy đủ, đầu vào là gì, đầu ra là gì và chỉ rõ sự kết thúc thuật toán.
- Cần mô tả thuật toán cho tốt thì người máy hay máy tính mới hiểu đúng và thực hiện được.
- Nếu không, kết quả thực hiện thuật toán có thể không như mong đợi.
Đúng 0
Bình luận (0)
Cho một xâu kí tự S chỉ toàn kí tự số 0 và 1. Biết rằng các kí tự số 0 đứng trước các ký tự số : 00....0011.....11.Yêu cầu: Hãy cho biết vị trí của ký tự số 0 cuối cùng trong dãy.Dữ liệu vào:Chứa xâu kí tự S (Độ dài của xâu S≤107 và luôn có ký tự số 0 và ký tự số 1)Kết quả:Một số nguyên dương là vị trí của ký tự số 0 cuối cùng trong dãy.Ví dụInputCopy0000011111OutputCopyLưu ý:Dùng C++
Đọc tiếp
Cho một xâu kí tự S chỉ toàn kí tự số 0 và 1. Biết rằng các kí tự số 0 đứng trước các ký tự số : 00....0011.....11.
Yêu cầu: Hãy cho biết vị trí của ký tự số 0 cuối cùng trong dãy.
Dữ liệu vào:
Chứa xâu kí tự S (Độ dài của xâu S≤107 và luôn có ký tự số 0 và ký tự số 1)
Kết quả:
Một số nguyên dương là vị trí của ký tự số 0 cuối cùng trong dãy.
Ví dụ
Input
Copy
0000011111
Output
Copy
Lưu ý:Dùng C++
var s:string;
i:integer;
begin
write('Nhap xau ki tu S = ');readln(s);
for i:=1 to length(s) do
begin
if s[i] <> '0' then write('Vi tri cua so 0 cuoi cung la ',i-1);
i:=length(s);
end;
readln;
end.
Đúng 1
Bình luận (0)
Nhập vào xâu ký tự số nhị phân có tối đa 16 bit. Tính và đưa ra giá trị của số nhị phân đó. Đưa ra màn hình số hex tương ứng với số nhị phân.Ngôn ngữ C++
1. Em hãy lấy một vài vd về hoạt động thông tin và hãy chỉ ra những hoạt động nào đã được thực hiện, các thông tin vào/ra trong các vd đó.
2. Biểu diễn kí tự c có số thứ tự 99 và kí tự m có số thứ tự 108 bằng dãy bít nhị phân.
3. Giả sử một bóng đèn có 2 trạng thái bật/tắt tương ứng với 2 kí hiệu 1 và 0. Vậy có 4 bóng đèn như vậy sẽ có bao nhiêu trạng thái? Em hãy biểu diễn các trạng thái tương ứng với 2 kí hiệu 1 và 0.
Đọc tiếp
1. Em hãy lấy một vài vd về hoạt động thông tin và hãy chỉ ra những hoạt động nào đã được thực hiện, các thông tin vào/ra trong các vd đó.
2. Biểu diễn kí tự c có số thứ tự 99 và kí tự m có số thứ tự 108 bằng dãy bít nhị phân.
3. Giả sử một bóng đèn có 2 trạng thái bật/tắt tương ứng với 2 kí hiệu 1 và 0. Vậy có 4 bóng đèn như vậy sẽ có bao nhiêu trạng thái? Em hãy biểu diễn các trạng thái tương ứng với 2 kí hiệu 1 và 0.
Mật khẩu của máy tính là một dãy các kí tự (có kể thứ tự từ trái qua phải) được chọn từ: 10 chữ số, 26 chữ cái in thường, 26 chữ cái in hoa và 10 kí tự đặc biệt. Bạn Ngân muốn lập một mật khẩu của máy tính có độ dài là 8 kí tự bao gồm: 4 kí tự đầu tiên là 4 chữ số đổi một khác nhau, 2 kí tự tiếp theo là chữ cái in thường, 1 kí tự tiếp theo nữa là chữ cái in hoa, kí tự cuối cùng là kí tự đặc biệt. Bạn Ngân có bao nhiêu cách lập một mật khẩu của máy tính?
Đọc tiếp
Mật khẩu của máy tính là một dãy các kí tự (có kể thứ tự từ trái qua phải) được chọn từ: 10 chữ số, 26 chữ cái in thường, 26 chữ cái in hoa và 10 kí tự đặc biệt. Bạn Ngân muốn lập một mật khẩu của máy tính có độ dài là 8 kí tự bao gồm: 4 kí tự đầu tiên là 4 chữ số đổi một khác nhau, 2 kí tự tiếp theo là chữ cái in thường, 1 kí tự tiếp theo nữa là chữ cái in hoa, kí tự cuối cùng là kí tự đặc biệt. Bạn Ngân có bao nhiêu cách lập một mật khẩu của máy tính?
+) Số cách chọn 4 kí tự đầu tiên là: \(A_{10}^4\) (cách chọn)
+) Số cách chọn 2 kí tự tiếp theo là: \(C_{26}^1.C_{26}^1\) (cách chọn)
+) Số cách chọn 1 kí tự tiếp theo là: \(C_{26}^1\) (cách chọn)
+) Số cách chọn 1 kí tự cuối cùng là: \(C_{10}^1\) (cách chọn)
+) Áp dụng quy tắc nhân, ta có số mật khẩu có thể tạo thành là:
\(A_{10}^4.C_{26}^1.C_{26}^1.C_{26}^1.C_{10}^1\) ( mật khẩu)
Đúng 0
Bình luận (0)
Cho một xâu S có N kí tự. Người ta viết các kí tự của xâu S lên vòng tròn theo chiều kim đồng hồ. Như vậy, nếu đi trên vòng tròn theo chiều kim đồng hồ thì kí tự thứ N+1 chính là kí tự thứ nhất của xâu S.
Xuất phát từ ký tự thứ nhất của xâu S trên vòng tròn, ta đếm từng ký tự theo chiều kim đồng hồ đến kí tự thứ K rồi cắt vòng tròn tại vị trí sau kí tự thứ K này, ta được một xâu mới R mà ký tự đầu tiên của xâu mới là kí tự thứ K+1.
Dữ liệu vào: Cho từ tệp văn bản DOIXAU.INP dòng đầu tiên là xâu...
Đọc tiếp
Cho một xâu S có N kí tự. Người ta viết các kí tự của xâu S lên vòng tròn theo chiều kim đồng hồ. Như vậy, nếu đi trên vòng tròn theo chiều kim đồng hồ thì kí tự thứ N+1 chính là kí tự thứ nhất của xâu S. Xuất phát từ ký tự thứ nhất của xâu S trên vòng tròn, ta đếm từng ký tự theo chiều kim đồng hồ đến kí tự thứ K rồi cắt vòng tròn tại vị trí sau kí tự thứ K này, ta được một xâu mới R mà ký tự đầu tiên của xâu mới là kí tự thứ K+1. Dữ liệu vào: Cho từ tệp văn bản DOIXAU.INP dòng đầu tiên là xâu S, dòng thứ 2 là số nguyên K(1 ≤ K ≤ 104). Kết quả: Ghi vào file DOIXAU.OUT xâu R.
Một xâu được gọi là chuẩn nếu đầu và cuối xâu không có ký tự trống, đồng thời
trong xâu không có 2 ký tự trống kề liền. Cho xâu S không quá 500 kí tự.
Yêu cầu: - Chuẩn hóa xâu đã nhập.
- Tìm số lượng kí tự chữ số trong xâu.
Dữ liệu vào: Xâu kí tự S.
Dữ liệu ra: Dòng 1: In ra xâu đã chuẩn hóa.
Dòng 2: In ra số lượng kí tự chữ số.














