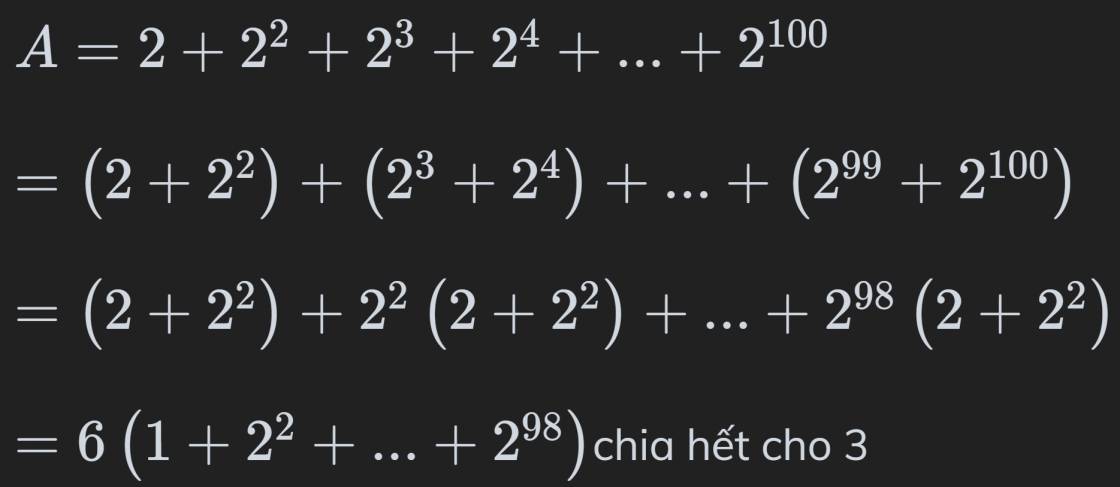\(B=3+3^2+3^3+3^4+...+3^{2009}+3^{2010}\)

\(=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\)

\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)

\(=4.\left(3+3^3+...+3^{2009}\right)\)

⇒ \(B\) ⋮ 4

b: \(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)=31\cdot\left(5+...+5^{2008}\right)⋮31\)

 53! - 51! = 51! x (52 x 53) - 51! (phân tích số 53! thành 51! x 52 x 53) 
= 51! x (2756 -1) 
= 51! x 2755 
2755 chia hết cho 29 nên suy ra 53! - 51! chia hết cho 29

 53! - 51!

= 1.2.3...28.29....53 - 1.2.3...28.29...51

=29 . ( 1.2.3...28.30.31...53 - 1.2.3...28.30.31...51) chia hết cho 29.

2275 không chia hết cho 29 nha Nguyễn Thiện Nhân

Bài 1:

\(a,A=\left(2+2^2\right)+\left(2^3+2^4\right)+...+\left(2^{2009}+2^{2010}\right)\\ A=\left(1+2\right)\left(2+2^3+...+2^{2009}\right)=3\left(2+...+2^{2009}\right)⋮3\\ A=\left(2+2^2+2^3\right)+...+\left(2^{2008}+2^{2009}+2^{2010}\right)\\ A=\left(1+2+2^2\right)\left(2+...+2^{2008}\right)=7\left(2+...+2^{2008}\right)⋮7\)

\(b,\left(\text{sửa lại đề}\right)B=\left(3+3^2\right)+\left(3^3+3^4\right)+...+\left(3^{2009}+3^{2010}\right)\\ B=\left(1+3\right)\left(3+3^3+...+3^{2009}\right)=4\left(3+3^3+...+3^{2009}\right)⋮4\\ B=\left(3+3^2+3^3\right)+...+\left(3^{2008}+3^{2009}+3^{2010}\right)\\ B=\left(1+3+3^2\right)\left(3+...+3^{2008}\right)=13\left(3+...+3^{2008}\right)⋮13\)

Bài 2:

\(a,\Rightarrow2A=2+2^2+...+2^{2012}\\ \Rightarrow2A-A=2+2^2+...+2^{2012}-1-2-2^2-...-2^{2011}\\ \Rightarrow A=2^{2012}-1>2^{2011}-1=B\\ b,A=\left(2020-1\right)\left(2020+1\right)=2020^2-2020+2020-1=2020^2-1< B\)

đúng rùi

a) => 5^5 - 5^4 + 5^3 = 5^3(5^2 - 5+1) = 5^3(25-5+1) = 5^3 x 21 = 5^3 x 3 x 7 chia hết cho 7

b) 81^7 - 27^9 - 9^13 = 3^28 - 3^27 - 3^26 = 3^26(3^2 - 3 - 1)= 3^26 x 5 = 3^24 x 45 chia hết cho 45

c) 16^5 + 2^15 = 2^20 + 2^15 = 2^15 (2^5 + 1) = 2^15 x 33 chia hết cho 33

d) = 51! x 52 x 53 - 51! = 51! x (52 x 53 - 1) = 51! x 2755. Vì 51! chia hết cho 45 nên 51! x 2755 chia hết cho 45

\(a,5.\left(5^2-5+1\right)=5.\left(25-5+1\right)=5.21=5.7.3\)

vì tích trên có chứa thừa số 7 nên tích đó chia hết cho 7

\(b,3^{28}-3^{27}-3^{26}=3^{24}.\left(3^4-3^3-3^2\right)=3^{24}.45\)

vì tích trên có chứa thừa số 45 nên tích đó chia hết cho 45

Ứ biết

a: \(B=3^1+3^2+...+3^{2010}\)

\(=3\left(1+3\right)+3^3\left(1+3\right)+...+3^{2009}\left(1+3\right)\)

\(=4\left(3+3^3+...+3^{2009}\right)⋮4\)

\(B=3\left(1+3+3^2\right)+...+3^{2008}\left(1+3+3^2\right)\)

\(=13\left(3+...+3^{2008}\right)⋮13\)

b: \(C=5^1+5^2+...+5^{2010}\)

\(=5\left(1+5\right)+...+5^{2009}\left(1+5\right)\)

\(=6\left(5+...+5^{2009}\right)⋮6\)

\(C=5\left(1+5+5^2\right)+...+5^{2008}\left(1+5+5^2\right)\)

\(=31\left(5+...+5^{2008}\right)⋮31\)

c: \(D=7\left(1+7\right)+...+7^{2009}\left(1+7\right)\)

\(=8\left(7+...+7^{2009}\right)⋮8\)

\(D=7\left(1+7+7^2\right)+...+7^{2008}\left(1+7+7^2\right)\)

\(=57\left(7+...+7^{2008}\right)⋮57\)

+) ta có : \(B=2+2^2+2^3+2^4+...+2^{100}\)

\(\Leftrightarrow B=\left(2+2^2+...+2^5\right)+\left(2^6+2^7+...+2^{10}\right)...+\left(2^{96}+2^{97}+2^{98}+2^{99}+2^{100}\right)\)

\(\Leftrightarrow B=2\left(1+2+...+2^4\right)+2^6\left(1+2+...+2^4\right)+...+2^{96}\left(1+2+...+2^4\right)\)

\(\Leftrightarrow B=2\left(31\right)+2^6\left(31\right)+...+2^{96}\left(31\right)=31\left(2+2^6+...+2^{96}\right)⋮31\left(đpcm\right)\)

+) ta có : \(C=53!-51!=53.52.51!-51!=51!\left(53.52-1\right)\)

\(\Leftrightarrow C=51!\left(2755\right)=29.95.51!⋮29\left(đpcm\right)\)