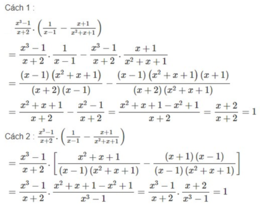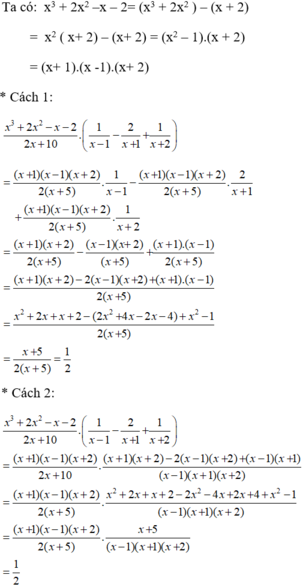công thức nào sau đây thể hiện tính chất phân phối của phép nhân đôiá với phếp cộng

Những câu hỏi liên quan
Công thức nào sau đây thể hiện tính chất phân phối của phép nhân đối với phép cộng?
A. a.(b+c)=a.b+a.c
B. a+(b+c)=(a+b)+c
C. a.b=b.a
D. (a.b).c=a.(b.c)
Xem thêm câu trả lời
Công thức thể hiện tính chất phân phối giữa phép nhân đối với phép cộng?
a(b+c)=ab+ac
dạng tổng quát của tinha chất giao goán , kết hợp của phép cộng , phép nhân , tính chất phân phối của phép nhân đối với phép công
*) Phép cộng
Giao hoán: a + b = b + a
Kết hợp: a + ( b + c) = (a + b) + c = a+b+c
Tính chất phân phối: a . b + a.c = a.(b + c)
*) Phép nhân:
Giao hoán: a . b = b . a
Kết hợp: a . (b . c) = (a . b) . c = a.b.c
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
-
1
x
+
2
.
1
x
-
1
-...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 - 1 x + 2 . 1 x - 1 - x + 1 x 2 + x + 1
Có thể tính nhẩm tích 45.6 bằng cách: Áp dụng tính chất kết hợp của phép nhân: 45.6 45.(2.3) (45.2).3 90 .3 270 Áp dụng tính chất phân phối của phép nhân đối với phép cộng: 45.6 (40+ 5).6 40.6 + 5.6 240 +30 270 Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng: 25.12; 34.11; 47.101
Đọc tiếp
Có thể tính nhẩm tích 45.6 bằng cách:
Áp dụng tính chất kết hợp của phép nhân:
45.6 = 45.(2.3) = (45.2).3 = 90 .3 = 270
Áp dụng tính chất phân phối của phép nhân đối với phép cộng:
45.6 = (40+ 5).6 = 40.6 + 5.6 = 240 +30 = 270
Hãy tính nhẩm bằng cách áp dụng tính chất phân phối của phép nhân đối với phép cộng:
25.12; 34.11; 47.101
Áp dụng tính chất phân phối của phép nhân đối với phép cộng: a(b+c)=ab+ac ta có:
25.12 = 25.(10 + 2) = 25.10 + 25.2 = 250 + 50 = 300.
34.11 = 34.(10 + 1) = 34.10 + 34 = 340 + 34 = 374.
47.101 = 47.(100 + 1) = 47.100 + 47.1 = 4700 + 47 = 4747.
Đúng 0
Bình luận (0)
1. Viết dạng tổng quát các tính chất giao hoán , kết hợp của phép cộng , phép nhân, tính chất phân phối của phép nhân đối với phép cộng.
2. Lũy thừa bậc n của a là gì ?
3. Viết công thức nhân hai lũy thừa cùng cơ số , chia hai lũy thừa cùng cơ số .
1.Phép cộng:
giao hoán: a + b = b + a
Kết hợp : (a + b) + c = a + ( b + c)
Phép nhân:
Giao hoán: a . b = b . a
Kết hợp: (a . b) . c = a( b . c)
2, Luỹ thừa bậc n của a là tích của n thừa số, mỡi thừa số bằng a
3, Nhân hai luỹ thừa cùng cơ số: an . am = an+m
chia hai luỹ thừa cùng cơ số: an : am = an-m ( n lớn hơn hoặc bằng m, n khác 0)
Đúng 1
Bình luận (0)
1
| tính chất | phép cộng | phép nhân | phép nhân và phép cộng | |
| giao hoán | a+b=b+a | a*b=b*a | k | |
| kết hợp | (a+b)+c=a+(b+c) | (A*b)*c=a*(b*c) | k | |
| phân phối | k co | k có | (a+b)*c=a*c+b*c | |
2 là n số tự nhiên a nhân với nhau
3 a^m/a^n=a^m-n ( phép chia )
a^m*a^n=a^m+n
Đúng 0
Bình luận (0)
Rút gọn biểu thức sau theo hai cách (sử dụng và không sử dụng tính chất phân phối của phép nhân đối với phép cộng).
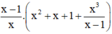
Cách 1:Không áp dụng tính phân phối:
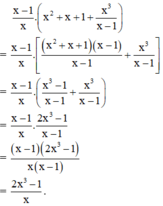
Cách 2: Áp dụng tính chất phân phối: A( B+ C)= AB + AC
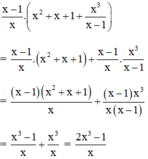
Đúng 0
Bình luận (0)
Cho biểu thức M = \(\frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\). Hãy tính giá trị của M theo 2 cách:
a) Thực hiện tính nhân rồi cộng 2 kết quả
b) Áp dụng tính chất phân phối của phép nhân đối với phép cộng
a)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{{ - 5}}{{56}} + \frac{{ - 11}}{{56}} = \frac{{ - 16}}{{56}} = \frac{{ - 2}}{7}\end{array}\)
b)
\(\begin{array}{l}M = \frac{1}{7}.(\frac{{ - 5}}{8}) + \frac{1}{7}.(\frac{{ - 11}}{8})\\ = \frac{1}{7}.[(\frac{{ - 5}}{8}) + (\frac{{ - 11}}{8})]\\ = \frac{1}{7}.\frac{{ - 16}}{8}\\ = \frac{1}{7}.( - 2)\\ = \frac{{ - 2}}{7}\end{array}\)
Đúng 0
Bình luận (0)
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này:
x
3
+
2
x
2
-
x
-
2
2
x
+
10
.
1
x...
Đọc tiếp
Thực hiện các phép tính sau bằng hai cách: dùng tính chất phân phối của phép nhân đối với phép cộng và không dùng tính chất này: x 3 + 2 x 2 - x - 2 2 x + 10 . 1 x - 1 - 2 x + 1 + 1 x + 2