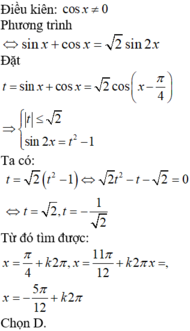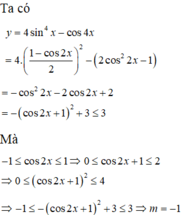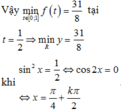3cos2x+8sin3xcosx+16cosx=4sin4x+22sinx+23

Những câu hỏi liên quan
giải pt:
3cos2x+8sin3xcosx+16cosx=4sin4x+22sinx+23
Giải phương trình
1
+
tan
x
2
2
sin
x
Đọc tiếp
Giải phương trình 1 + tan x = 2 2 sin x
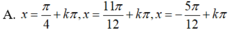
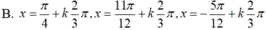
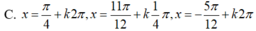
![]()
Giải phương trình
sin
x
+
cos
x
2
2
sin
x
cos
x
Đọc tiếp
Giải phương trình sin x + cos x = 2 2 sin x cos x
![]()

![]()
![]()
4sin4x+2cos2x-\(\dfrac{1}{4}\)cos4x
Tìm các họ nghiệm của phương trình:
tan
2
x
+
tan
x
tan
2
x
+
1
2
2
sin
x
+...
Đọc tiếp
Tìm các họ nghiệm của phương trình: tan 2 x + tan x tan 2 x + 1 = 2 2 sin x + π 4
A. x = - π 4 + k π 2 x = π 6 + k 2 π x = 5 π 6 + k 2 π
B. x = π 4 + k π x = π 6 + k 2 π x = - 5 π 6 + k 2 π
C. x = π 4 + k π x = π 6 + k 2 π x = 5 π 6 + k 2 π
D. x = - π 4 + k π x = π 6 + k 2 π x = 5 π 6 + k 2 π
Điều kiện cos x ≠ 0 ⇔ x ≠ π 2 + k π .
Phương trình đã cho tương đương:
tan 2 x + tan x cos 2 x = 1 2 sin x + cos x ⇔ sin 2 x + sin x cos x = 1 2 sin x + cos x ⇔ 2 sin 2 x + sin 2 x = sin x + cos x ⇔ 2 sin x sin x + cos x = sin x + cos x ⇔ sin x + cos x 2 sin x - 1 = 0 ⇔ sin x + cos x = 0 2 sin x - 1 = 0 ⇔ tan x = - 1 sin x = 1 2 ⇔ x = - π 4 + k π x = π 6 + k 2 π x = 5 π 6 + k 2 π
Đáp án D
Đúng 0
Bình luận (0)
cos^3x*sinx-sin^3x*cosx=1/4sin4x
Cho 4sin4x + 3cos4x = 7/4 .Tính A = 3sin4x + 4cos4x
Ta có:
\(\left\{{}\begin{matrix}sin^2x+cos^2x=1\\4sin^4x+3cos^4x=\dfrac{7}{4}\end{matrix}\right.\)
\(\Rightarrow4sin^4x+3\left(1-sin^2x\right)^2=\dfrac{7}{4}\)
\(\Leftrightarrow7sin^4x-6sin^2x+\dfrac{5}{4}=0\) \(\Rightarrow\left[{}\begin{matrix}sin^2x=\dfrac{1}{2}\Rightarrow cos^2x=\dfrac{1}{2}\\sin^2x=\dfrac{5}{14}\Rightarrow cos^2x=\dfrac{9}{14}\end{matrix}\right.\)
Do đó: \(\left[{}\begin{matrix}A=\dfrac{7}{4}\\A=\dfrac{57}{28}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Tìm giá trị nhỏ nhất m của hàm số y = 4 sin 4 x - cos 4 x ?
A. m = -3
B. m = -1
C. m = 3
D. m = 5
Giá trị nhỏ nhất của hàm số
y
4
sin
4
x
+
cos
2
x
+
3
bằng: A.
31
8
B.5 C.4 D.
24
5
Đọc tiếp
Giá trị nhỏ nhất của hàm số y = 4 sin 4 x + cos 2 x + 3 bằng:
A. 31 8
B.5
C.4
D. 24 5