
sẵn vẽ hình ở 3 câu dưới nha
BÂY GIỜ CÁC BẠN HÃY TƯỞNG TƯỢNG RỒI VẼ LẠI CHO MÌNH 4 HÌNH LẬP PHƯƠNG CẠNH 2 CM , 1 HÌNH Ở TRÊN , 3 HÌNH Ở DƯỚI , GIÚP MÌNH NHA RỒI MÌNH CHO ĐỀ BÀI NHA
banh chụp hình vào
Câu 6 Vị trí hình chiếu đứng ở trên bản vẽ là:
A. Ở góc trên bên phải bản vẽ. C. Ở góc trên bên trái bản vẽ.
B. Ở góc dưới bên trái bản vẽ. D. Ở góc dưới bên phải bản vẽ.
Câu 7. Khối đa diện được bao bởi:
A. Các hình vuông. C. Các hình đa giác phẳng.
B. Các hình tam giác. D. Các hình chữ nhật.
Câu 8 Hình chiếu đứng là tam giác cân, hình chiếu bằng là hình tròn. Đó là các hình chiếu của :
A. Hình nón. C. Hình trụ.
B. Hình lăng trụ đều. D. Hình cầu.
Câu 9 Khi quay………………..một vòng quanh một cạnh cố định, ta được hình trụ.
Cụm từ điền vào chỗ (…) của câu trên là:
A. hình tam giác cân C. nửa hình tròn
B. hình tam giác vuông D. hình chữ nhật
Câu 10 Nét gạch chấm mảnh dùng để biểu diễn:
A. Cạnh thấy, đường bao thấy. B. Đường dóng, đường kích thước.
C. Đường tâm, đường trục đối xứng. D. Cạnh khuất, đường bao khuất.
bạn ơi câu hỏi mik nhập sẵn ở dưới rùi đó bạn giúp mik với


Giải câu b nha giải giống như mẫu ở hình dưới câu a nhé
b: (d) cắt trục tung tại điểm có tung độ là -3 và cắt trục hoành tại điểm có hoành độ là 2
Gọi (d): y=ax+b(a<>0) là phương trình đường thẳng cần tìm
Vì (d) cắt trục tung tại điểm có tung độ là -3 nên thay x=0 và y=-3 vào (d), ta được:
\(a\cdot0+b=-3\)
=>b=-3
=>(d): y=ax-3
Vì (d) cắt trục hoành tại điểm có hoành độ là 2 nên thay x=2 và y=0 vào (d), ta được:
\(2\cdot a-3=0\)
=>2a-3=0
=>2a=3
=>\(a=\dfrac{3}{2}\)
Vậy: (d): \(y=\dfrac{3}{2}x-3\)
Để sao chép màu từ một màu có sẵn trên hình vẽ, em chọn công cụ nào dưới đây trong hộp công cụ?
A. 
B.
C. 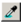
D. 
Để sao chép màu từ một màu có sẵn trên hình vẽ, em chọn công cụ nào dưới đây trong hộp công cụ?
A. 
B.
C. 
D.
Câu nào dưới đây viết về hai lực tác dụng lên hai vật A và B vẽ ở hình dưới đây là đúng?
A. Hai lực này là hai lực cân bằng.
B. Hai lực này cùng phương, ngược chiều, có cường độ bằng nhau
C. Hai lực này khác phương, cùng chiều, có cường độ bằng nhau.
D. Hai lực này cùng phương, cùng chiều, có cường độ bằng nhau.
B
Hai lực tác dụng lên hai vật A và B vẽ ở hình vẽ là hai lực này cùng phương, ngược chiều, có cường độ bằng nhau.
a/ \(\lim\limits_{x\rightarrow3}\dfrac{\sqrt[3]{x^2-1}-2}{x-3}+\lim\limits_{x\rightarrow3}\dfrac{2-\sqrt[4]{1+5x}}{x-3}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{x^2-1-8}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{16-1-5x}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4.\sqrt[3]{1+5x}+8\right)}\)
\(=\lim\limits_{x\rightarrow3}\dfrac{\left(x-3\right)\left(x+3\right)}{\left(x-3\right)\left(\sqrt[3]{\left(x^2-1\right)^2}+2.\sqrt[3]{x^2-1}+4\right)}+\lim\limits_{x\rightarrow3}\dfrac{-5\left(x-3\right)}{\left(x-3\right)\left(\sqrt[4]{\left(1+5x\right)^3}+2\sqrt[3]{\left(1+5x\right)^2}+4\sqrt[3]{1+5x}+8\right)}\)
\(=\dfrac{3+3}{\sqrt[3]{\left(3^2-1\right)^2}+2.\sqrt[3]{3^2-1}+4}-\dfrac{5}{\sqrt[4]{\left(1+5.3\right)^3}+2\sqrt[3]{\left(1+5.3\right)^2}+4.\sqrt[3]{1+5.3}+8}=\dfrac{11}{32}\)
\(\Rightarrow a^2+b^2=1145\)
40/
\(L=\lim\limits_{x\rightarrow0}\dfrac{af\left(x\right)+b^n-b^n}{f\left(x\right)\left[\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+....+b^{n-1}\right]}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-1}}+b.\sqrt[n]{\left(af\left(x\right)+b^n\right)^{n-2}}+...+b^{n-1}}\)
\(L=\lim\limits_{x\rightarrow0}\dfrac{a}{b^{n-1}+b^{n-1}++...+b^{n-1}}=\dfrac{a}{nb^{n-1}}\)
40/
\(\sqrt{1+ax}.\sqrt[3]{1+bx}+\sqrt[4]{1+cx}-1=\left(\sqrt{1+ax}-1\right)+\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)+\sqrt{1+ax}.\sqrt[3]{1+bx}.\left(\sqrt[4]{1+cx}-1\right)\)
\(=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}-1}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(\sqrt[3]{1+bx}-1\right)}{x}+\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}.\sqrt[3]{1+bx}\left(\sqrt[4]{1+cx}-1\right)}{x}\)
\(I_1=\lim\limits_{x\rightarrow0}\dfrac{1+ax-1}{x\left(\sqrt{1+ax}+1\right)}=\dfrac{a}{\sqrt{1+ax}+1}=\dfrac{a}{2}\)
\(I_2=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\left(1+bx-1\right)}{x\left(\sqrt[3]{\left(1+bx\right)^2}+\sqrt[3]{1+bx}+1\right)}=\dfrac{b\sqrt{1+ax}}{\sqrt[3]{\left(1+bx\right)^2+\sqrt[3]{1+bx}+1}}=\dfrac{b}{3}\)
\(I_3=\lim\limits_{x\rightarrow0}\dfrac{\sqrt{1+ax}\sqrt[3]{1+bx}\left(1+cx-1\right)}{x\left(\sqrt[4]{\left(1+cx\right)^3}+\sqrt[3]{\left(1+cx\right)^2}+\sqrt[3]{1+cx}+1\right)}=\dfrac{c}{4}\)
\(\Rightarrow L=\dfrac{a}{2}+\dfrac{b}{3}+\dfrac{c}{4}\)
P/s: Thông cảm mình đang đau đầu nên làm hơi lâu :b
Cho hình thang ABCD ( xem hình vẽ) , biết diện tích hình tam giác AED là 4cm vuông và diện tích hình tam giác BHC là 6 cm vuông. Tính diện tích hình tứ giác MHNE ( hình vẽ mình vẽ ở dưới nha )
Nối đường cao DH, NK, H,K nằm trên đường thẳng AB, ta có:
Diện tích tam giác DAM = DH.AM/2
Diện tích tam giác AMN = NK.AM/2
Mà DH=NK=> S(DAM) = S(AMN)
Mà S(DAM) = S(AEM) + S(AED), S(AMN) = S(AEM) + S(EMN)
=> S(AED)=S(EMN) = 2cm2
So sánh tương tự đối với S(MNF) và S(BFC) => S(MNF) = S(BFC) = 3cm2
Mà S(MENF)= S(EMN) + S(MNF) = 2+3 = 5cm2