Cho hình bình hành ABCD, trên cạnh AB lấy M, trên cạnh BC lấy N.
a) Chứng minh : SADN=SDMC
b) Gọi I là giao AN,CM. Chứng minh nếu AN=CM thì \(\widehat{AID}=\widehat{DIC}\)
Cho hình bình hành ABCD , trên cạnh AB lấy điểm M , trên cạnh BC lấy điểm N sao cho AN = CM. Gọi giao điểm của AN và CM là K . Chứng minh KD là tia phân giác của góc AKC.
Trước hết ta chứng minh bổ đề sau (nếu em chưa học)
Cho 4 điểm A; B; C; D phân biệt sao cho \(AB||CD\), khi đó ta luôn có: \(S_{\Delta ACD}=S_{\Delta BCD}\)
C/m: từ A và B lần lượt kẻ \(AH\) và \(BK\) vuông góc CD \(\Rightarrow AH||BK\Rightarrow\) tứ giác AHKB là hình chữ nhật
\(\Rightarrow AH=BK\)
Do \(\left\{{}\begin{matrix}S_{\Delta ACD}=\dfrac{1}{2}AH.CD\\S_{\Delta BCD}=\dfrac{1}{2}BK.CD\end{matrix}\right.\) mà \(AH=BK\Rightarrow S_{\Delta ACD}=S_{\Delta BCD}\) (đpcm)
Quay lại bài toán, áp dụng bổ đề trên ta có: do N thuộc BC nên \(NC||AD\Rightarrow S_{\Delta NAD}=S_{\Delta CAD}\) (1)
Tương tự, \(AM||CD\Rightarrow S_{\Delta ACD}=S_{\Delta MCD}\) (2)
(1);(2) \(\Rightarrow S_{\Delta NAD}=S_{\Delta MCD}\)
Từ D lần lượt kẻ \(DE\perp AN\) và \(DF\perp CM\)
\(\Rightarrow\left\{{}\begin{matrix}S_{\Delta NAD}=\dfrac{1}{2}DE.AN\\S_{\Delta MCD}=\dfrac{1}{2}DF.CM\end{matrix}\right.\)
Mà \(\left\{{}\begin{matrix}S_{\Delta NAD}=S_{\Delta MCD}\\AN=CM\end{matrix}\right.\) \(\Rightarrow DE=DF\)
\(\Rightarrow\Delta_VDEK=\Delta_VDFK\left(ch-cgv\right)\)
\(\Rightarrow\widehat{EKD}=\widehat{FKD}\) hay KD là phân giác
a: Xét tứ giác BMDN có
BM//DN
BM=DN
Do đó: BMDN là hình bình hành
b: AM+MB=AB
CN+ND=CD
mà MB=ND và AB=CD
nên AM=CN
Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
c: AMCN là hình bình hành
=>AN//CM
=>NK//MH
BMDN là hình bình hành
=>BN//DM
=>NH//KM
Xét tứ giác MKNH có
MK//NH
MH//NK
Do đó: MKNH là hình bình hành
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh DC lấy điểm N sao cho AM = CN.
a) Chứng minh AN//CM ;
b) Gọi O là giao điểm của AC và BD. Chứng minh O là trung điểm của MN.
a: Xét tứ giác AMCN có
AM//CN
AM=CN
Do đó: AMCN là hình bình hành
b:ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AMCN là hình bình hành
=>AC cắt MN tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của MN
Cho hình bình hành ABCD. Trên cạnh AB và BC lần lượt lấy hai điểm M và N sao cho AN=CM. Gọi K là giao điểm của AN và CM. CMR: KD là tia phân giác \(\widehat{AKC}\)
Cho hình bình hành ABCD. Trên cạnh AB lấy điểm M, trên cạnh DC lấy điểm N sao cho AM=CN.
a/ Chứng minh AN//CM.
b/ Gọi O là giao điểm của AC và BD. Chứng minh O là trung điểm của MN.
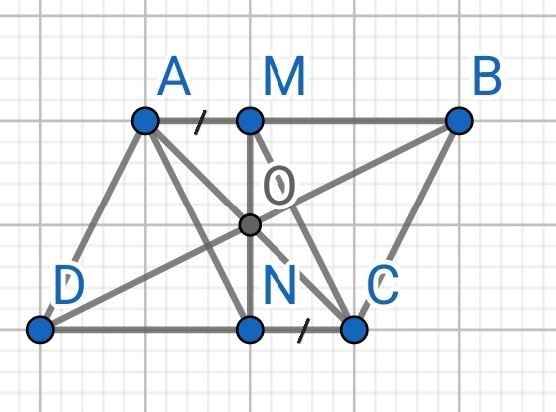 a) Do ABCD là hình bình hành
a) Do ABCD là hình bình hành
AB // CD
⇒ AM // CN
Tứ giác AMCN có:
AM // CN (cmt)
AM = CN (gt)
⇒ AMCN là hình bình hành
⇒ AN // CM
b) Do ABCD là hình bình hành
O là giao điểm của AC và BD
⇒ O là trung điểm của AC
Lại có AMCN là hình bình hành
O là trung điểm của AC (cmt)
⇒ O là trung điểm của MN
Cho Tam giác ABC cân tại A trên cạnh AB lấy M trên AC lấy N sao cho AM = AN . Gọi E là giao điểm của CM và BN
a) chứng minh BN = CM
b) chứng minh IBC cân
c) MN // BC
a) Xét ΔBMC và ΔCNB có :
BM=CN ( AB=AC; AM=AN )
góc B = góc C ( ΔABC cân tại A )
BC : chung
suy ra : hai Δ trên bằng nhau theo trường hợp ( c-g-c )
suy ra : đpcm
b) chứng minh EBC cân nha em
Từ : ΔBMC = ΔCNB
suy ra : góc MCB = góc NBC ( 2 góc tương ứng )
suy ra : đpcm
c) ta có : ΔABC cân tại A
suy ra : góc B = góc C= \(\dfrac{180-A}{2}\) (1)
ta lại có : ΔAMN cân tại A
suy ra : góc AMN = góc ANM = \(\dfrac{180-A}{2}\) (2)
Từ (1) và (2) suy ra đpcm do (các góc ở vị trí đồng vị và bằng nhau )
Cho tam giác ABC cân tại B. Trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N sao cho BM = BN.
a/ Chứng minh MN song song với AC.
b/ Gọi I là giao điểm của AN và CM. Chứng minh BI vuông góc với MN.
Cho tam giác ABC cân tại B. Trên cạnh AB lấy điểm M, trên cạnh BC lấy điểm N sao cho BM = BN.
a/ Chứng minh MN song song với AC.
b/ Gọi I là giao điểm của AN và CM. Chứng minh BI vuông góc với MN.
Hình bạn tự vẽ
a, Nối M với N
Xét △BMN có:
BM=BN(gt)
=>△BMN cân tại B
=>∠BMN=(1800 - ∠B) / 2 (1)
Mà ∠BAC=(1800 - ∠B) / 2 (△ABC cân tại B) (2)
Từ (1) và (2) => ∠BMN=∠BAC (3)
Mà ∠BMN đồng vị ∠BAC (4)
Từ (3) và (4) => MN//AC
b, Xét △CMB và △ANB có
\(\left\{{}\begin{matrix}\text{AB = AC (△ABC cân tại B)}\\\text{∠ABC chung}\\\text{BM=BN}\left(gt\right)\end{matrix}\right.\)
=>△CMB = △ANB (c.g.c)
=> ∠BMC = ∠BNC
=>∠BMN + ∠CMN = ∠BNM + ∠MNA
Mà ∠BMN = ∠BNM (△BMN cân tại B)
=>∠BMN + ∠CMN = ∠BMN + ∠MNA
=> ∠CMN = ∠MNA
=> △IMN cân tại I
=> MI=NI (5)
Mà BM = BN (6)
Từ (5) và (6) => BI là đường trung trực của MN
=> BI ⊥ MN
Có gì không hiểu bạn cứ hỏi mình ![]()