Lời giải:

$S=10.11+11.12+12.13+...+29.30$

$3S=10.11(12-9)+11.12(13-10)+12.13(14-11)+...+29.30(31-28)$

$=(10.11.12+11.12.13+12.13.14+...+29.30.31)-(9.10.11+10.11.12+...+28.29.30)$

$=29.30.31-9.10.11=25980$

$\Rightarrow S=8660$

=1- 1/2 +1/2- 1/3+....+1/9- 1/10

=1- 1/10

=9/10

1/1x2 + 1/2x3 + 1/3x4 +...+1/9x10 = 1/1 - 1/2 + 1/2 -1/3 + 1/3 -1/4 +...+1/9-1/10

=1+( 1/2 -1/2)+(1/3-1/3)+...+(1/9-1/9)-1/10

=1 + 0 + 0 +...-1/10 = 9/10

\(\frac{1}{1x2}+\frac{1}{2x3}+\frac{1}{3x4}+....+\frac{1}{9x10}=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{9}-\frac{1}{10}=\)\(1-\frac{1}{10}=\frac{9}{10}\) chúc bạn học tốt tk mk nha

\(=\left(\dfrac{2}{11}+\dfrac{4}{11}-\dfrac{6}{11}\right)-\left(\dfrac{3}{8}-\dfrac{5}{8}\right)=0+\dfrac{2}{8}=\dfrac{2}{8}\)

=(\(\dfrac{2}{11}\)+\(\dfrac{4}{11}\)−\(\dfrac{6}{11}\)) − (\(\dfrac{3}{8}\)−\(\dfrac{5}{8}\)) = 0 + \(\dfrac{2}{8}\) = \(\dfrac{2}{8}\)

_HT_

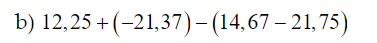
\(12,25+\left(-21,37\right)-\left(14,67-21,75\right)\)

\(=12,25-21,37-14,67+21,75\)

\(=12,25+21,75-21,37-14,63-0,04\)

\(=34-36-0,04\)

= -2-0,04=-2,04

120:{54-[50:2.(3^2-2.4)]}

= 120:{ 54-[25.(9-8)]}

= 120:{54-[25.1]}

= 120:{54-25}

= 120:29

=\(\dfrac{120}{29}\)

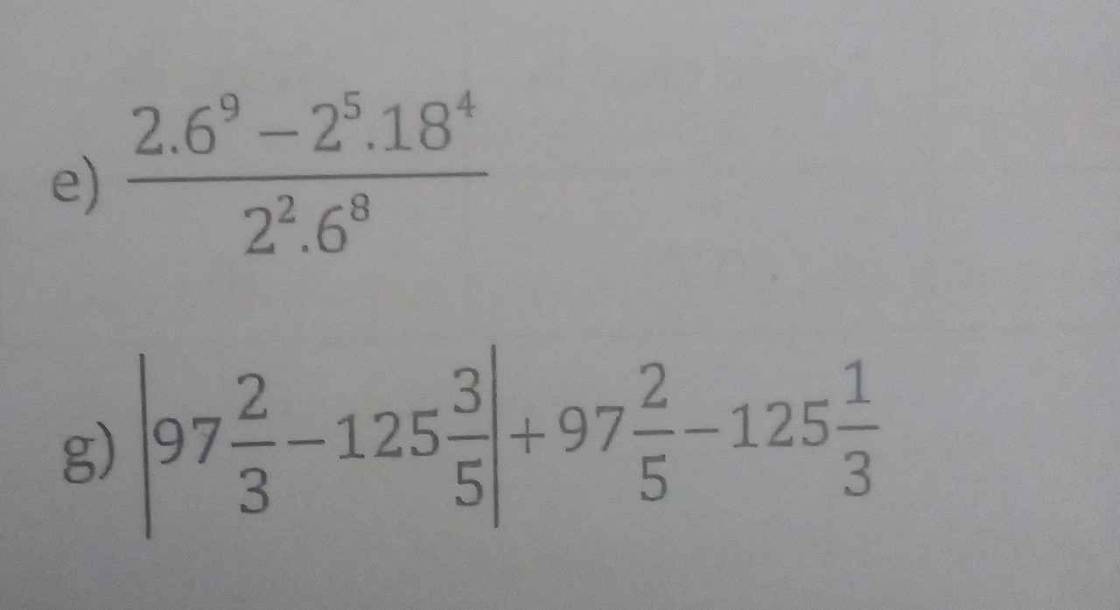
e: \(=\dfrac{2^{10}\cdot3^9-2^9\cdot3^8}{2^{10}\cdot3^8}=\dfrac{2^9\cdot3^8\left(2\cdot3-1\right)}{2^{10}\cdot3^8}=\dfrac{5}{2}\)

g: \(=125+\dfrac{3}{5}-97-\dfrac{2}{3}+97+\dfrac{2}{5}-125-\dfrac{1}{3}=0\)

\(\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{323}\\ =\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{17\times19}\right)\\=\dfrac{1}{2}\times\left(\dfrac{1}{1}-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{17}-\dfrac{1}{19}\right)\\ =\dfrac{1}{2}\times\left(\dfrac{1}{1}-\dfrac{1}{19}\right)\\ =\dfrac{1}{2}\times\dfrac{18}{19}=\dfrac{9}{19}\)

đề bài đây: 

\(\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+...+\dfrac{1}{323}\)