Cho tam giác ABC vuông tại A. Kẻ AH vuông góc với BC (H BC). Chứng minh rằng:
Cho tam giác ABC vuông tại A. Gọi BD là tia phân giác của góc B (D thuộc
AC). Kẻ DE vuông góc với BC (E thuộc BC)
a) Chứng minh rằng ∆ADB = ∆eDB
b) Chứng minh rằng BD là đường trung trực của đoạn thẳng AE.
c) Kẻ AH vuông góc với BC tại H (H thuộc BC). AH cắt BD tại I. Chứng minh tam
giác AID cân.
d) Chứng minh BD vuông góc với CA
e) Chứng minh ba đường thẳng BA, ED, CA đồng quy
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔBAD=ΔBED
b: ta có: ΔBAD=ΔBED
=>AB=BE và DA=DE
Ta có: BA=BE
=>B nằm trên đường trung trực của AE(1)
ta có: DA=DE
=>D nằm trên đường trung trực của AE(2)
Từ (1),(2) suy ra BD là đường trung trực của AE
c: ta có: \(\widehat{BIH}=\widehat{AID}\)(hai góc đối đỉnh)
\(\widehat{BIH}+\widehat{IBH}=90^0\)(ΔHBI vuông tại H)
Do đó: \(\widehat{AID}+\widehat{DBC}=90^0\)
Ta có: \(\widehat{AID}+\widehat{DBC}=90^0\)
\(\widehat{ADI}+\widehat{ABD}=90^0\)(ΔABD vuông tại A)
mà \(\widehat{DBC}=\widehat{ABD}\)
nên \(\widehat{ADI}=\widehat{AID}\)
=>ΔADI cân tại A
Cho tam giác ABC vuông tại A, kẻ AH vuông góc với BC . (H∈BC)
a) Chứng minh rằng ∠BAH=∠ACB
b) Tia phân giác của góc BAH cắt BC tại D. Chứng minh rằng ∠CDA=∠CAD
Cho tam giác ABC nhọn, kẻ đường cao AH (H thuộc cạnh BC). Tia phân giác của góc ABH cắt AH tại I. Qua A kẻ đường thẳng vuông góc với AB, cắt tia BI tại K. Kẻ KD vuông góc với BC (D thuộc BC). a) Chứng minh rằng: tam giác AKD cân. b) Chứng minh rằng: BK vuông gióc với AD . Từ đó suy ra I là trực tâm của tam giác ABD. c) Trên tia đối của tia HA lấy điểm E sao cho HE = HI. Chứng minh rằng AKDE là hình thang cân. d) Nếu biết rằng ADE 3ADK , tính số đo ABC.
Cho tam giác ABC vuông tại A, đường phân giác BD. Kẻ AE vuông góc với BD cắt BC tại K.
a. Chứng minh: Tam giác ABK cân tại B
b. Chứng minh rằng: DK vuông góc với BC.
c. Kẻ AH vuông góc với BC. Chứng minh rằng: AK là tia phân giác của góc HAC.
d. Gọi I là giao điểm của AH và BD. Chứng minh rằng: IK // AC.
a. Xét Δ ABE và Δ KBE có:
^B1=^B2(BD là tia p/g)
^BEA=^KEB=90o
AE chung
=> ΔABE=ΔKBE(g.c.g)
=>AB=KB
=>ΔABK cân tại B
(xin lỗi mình ko biết phần b,c,d) ;-;
cho bạn cái hình nè :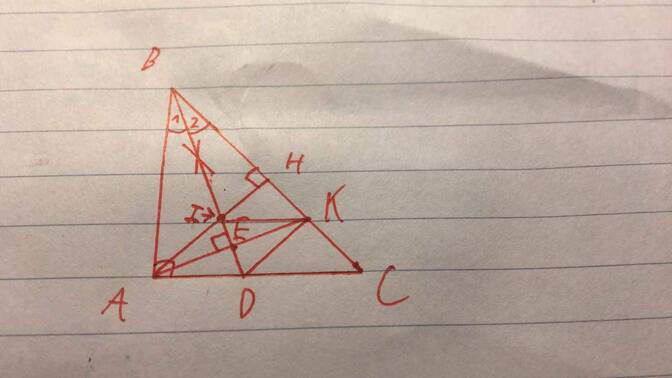
Cho tam giác ABC cân tại A. Kẻ AH vuông góc với BC .(h thuộc bc)
a. Chứng minh: tam giác ahb= tam giác ahc.
b. Từ điểm H kẻ HK vuông góc với AB tại K, HF vuông góc với AC tại F.
Chứng minh: hk=hf.
c. Chứng minh:kf song song bc
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
Do đó: ΔAHB=ΔAHC
b: Xét ΔAKH vuông tại K và ΔAFH vuông tại F có
AH chung
\(\widehat{KAH}=\widehat{FAH}\)
Do đó: ΔAKH=ΔAFH
Suy ra: HK=HF
c: Xét ΔABC có AK/AB=AF/AC
nên KF//BC
Cho tam giác ABC, có AH vuông góc với BC tại H. Chứng minh rằng: a)AH<1/2(AB + AC); b) Kẻ BK vuông góc AC tại K, CL vuông góc với AB tại L. Chứng minh: AH + BK + CL < AB + BC + CA.
đang cần gấp
Cho tam giác nhọn ABC. Về phía ngoài △ABC, vẽ các tam giác vuông cân tại A là tam giác ABD và tam giác ACE. Kẻ AH vuông góc với BC (H ∈ BC). Gọi I là giao điểm H A và DE.
a) Kẻ DN và EM vuông góc với H A (N, M ∈ H A). Chứng minh rằng DN = AH, EM = AH.
b) Chứng minh rằng DI = IE.
a/
Ta có
\(DN\perp HA\left(gt\right);BC\perp HA\left(gt\right)\) => DN//BC
\(\Rightarrow\widehat{NDB}+\widehat{CBD}=180^o\) (Hai góc trong cùng phía bù nhau)
\(\Rightarrow\widehat{NDA}+\widehat{ADB}+\widehat{ABD}+\widehat{ABC}=180^o\)
Ta có
tg ABD vuông cân tại A \(\Rightarrow\widehat{ADB}=\widehat{ABD}=45^o\Rightarrow\widehat{ADB}+\widehat{ABD}=90^o\)
\(\Rightarrow\widehat{NDA}+\widehat{ABC}=180^o-90^o=90^o\)
Xét tg vuông ABH
\(\widehat{BAH}+\widehat{ABC}=90^o\)
\(\Rightarrow\widehat{NDA}=\widehat{BAH}\)
Xét tg vuông NDA và tg vuông BAH có
\(\widehat{NDA}=\widehat{BAH}\left(cmt\right)\)
AD=AB (cạnh bên tg cân)
=> tg NDA = tg BAH (Hai tg vuông có cạnh huyền và góc nhọn tương ứng bằng nhau)
=> DN = AH
C/m tương tự ta cũng có tg vuông MAE = tg vuông CHA => EM=AH
b/
Ta có
\(DN\perp HA\left(gt\right);EM\perp HA\left(gt\right)\) => DN//EM
Xét tg vuông DIN và tg vuông EIM có
DN=EM (cùng bằng AH)
\(\widehat{IDN}=\widehat{IEM}\) (góc so le trong)
=> tg DIN = tg EIM (Hai tg vuông có 1 cạnh góc vuông và góc nhọn tương ứng bằng nhau)
=> DI=IE
Cho tam giác ABC vuông tại A ,kẻ Ah vuông góc với BC (H thuộc BC).Trên nửa mp bờ là đthẳng BC ko chứa điểm A vẽ tia Bx song song với AH .Trên tia Bx lấy D sao cho BD = AH .a. Chứng minh Cho tam giác ABC vuông tại A ,kẻ Ah vuông góc với BC (H thuộc BC).Trên nửa mp bờ là đthẳng BC ko chứa điểm A vẽ tia Bx song song với AH .Trên tia Bx lấy D sao cho BD = AH .
a. Chứng minh tam giác AHB và tam giác DHB bằng nhau
b. Gọi I là giao điểm của BH và DA .Chứng minh IB =IH
cho tam giác abc vuông tại a . biết ab = 3cm, bc=5cm.
a) tính ac?
b) kẻ phân giác bd. kẻ ah vuông góc bd tại h. kéo dài ah cắt bc tại e. chứng minh tam giác abh = tam giác ebh.
c) chứng minh rằng de vuông góc với bc.
d)hai đường thẳng ab và de cắt nhau tại k. chứng minh rằng tam giác bck cân
a) Áp dụng Pytago dễ dàng tính được AC=4
b) Xét hai tam giác vuông ABD và HBD có
BD cạnh chung
góc ABD = góc HBD (BD là phân giác góc B)
Nên hai tam giác trên bằng nhau (cạnh huyền - góc nhọn)
Suy ra AB = BH
AD = DH
Suy ra BD là trung trực của AH (định lý 2)
c) Ý bạn là E là giao điểm của AH và BD?
Hay E là giao điểm của DH và AB?
Cho tam giác ABC vuông tại A, phân giác BD . Kẻ DE vuông góc với BC.a) chứng minh rằng: tam giác ABD= tam giác EBD.b) kẻ AH vuông góc với BC,AH cắt BD tại I.Chứng minh rằng: AH song song với DE,tam giác AID cân
a) Ta có $\angle ABD = \angle EBD$ (vì BD là phân giác của góc $\angle ABC$), và $\angle ADB = \angle EDB = 90^\circ$ (vì DE vuông góc với BC). Vậy tam giác ABD và tam giác EBD có cặp góc đồng nhất, nên chúng bằng nhau theo trường hợp góc - góc - góc của các tam giác đồng dạng. Do đó, ta có tam giác ABD = tam giác EBD.
b) Ta cần chứng minh AH song song với DE, và tam giác AID cân.
Ta có $\angle ABD = \angle EBD$ (theo phần a)), và $\angle ADB = \angle EDB = 90^\circ$ (vì DE vuông góc với BC). Vậy tam giác ABD và tam giác EBD đồng dạng. Do đó:
$$\frac{AB}{EB} = \frac{BD}{BD} = 1$$
$$\Rightarrow AB = EB$$
Mà $AH$ là đường cao của tam giác $ABC$, nên $AB = AH \cos(\widehat{BAC})$. Tương tự, ta có $EB = ED \cos(\widehat{BAC})$. Vậy:
$$\frac{AH}{ED} = \frac{AB}{EB} = 1$$
Do đó, $AH = ED$, hay $AH$ song song với $DE$.
Tiếp theo, ta chứng minh tam giác $AID$ cân. Ta có:
$$\angle AID = \angle BID - \angle BIA = \frac{1}{2} \angle ABC - \angle BAC$$
Mà $\angle ABC = 90^\circ + \angle BAC$, nên:
$$\angle AID = \frac{1}{2}(90^\circ + \angle BAC) - \angle BAC = \frac{1}{2}(90^\circ - \angle BAC)$$
Tương tự, ta có:
$$\angle ADI = \frac{1}{2} \angle ADB = \frac{1}{2} \cdot 90^\circ = 45^\circ$$
Vậy tam giác $AID$ có hai góc bằng nhau là $\angle AID$ và $\angle ADI$, nên đó là tam giác cân.
Vậy, ta đã chứng minh được rằng $AH$ song song với $DE$, và tam giác $AID$ cân.
a: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔABD=ΔEBD
b: AH vuông góc BC
DE vuông góc BC
=>AH//DE