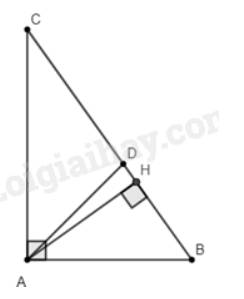
Cho tam giác ABC vuông tại A và có đường cao AH = 3cm. Vẽ đường tròn (A ; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt AC ở E.
Mọi người vẽ hình giùm emvới em cảm ơn nhiều

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có AB 4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D
Cho tam giác ABC vuông tại A có AB4cm, AC3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D.
a) Tính độ dài đoạn thẳng AH
b) Chứng minh BD là tiếp tuyến của đường tròn (C)
c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua...
Đọc tiếp
Cho tam giác ABC vuông tại A có AB = 4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D Cho tam giác ABC vuông tại A có AB=4cm, AC=3cm, đường cao AH. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường trong (C) tại điểm thứ 2 là D. a) Tính độ dài đoạn thẳng AH b) Chứng minh BD là tiếp tuyến của đường tròn (C) c) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA,BD thứ tự E,F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB,BD lần lượt tại P,Q. Chứng minh EF bình phương =4PE.QF
a:\(BC=\sqrt{4^2+3^2}=5\left(cm\right)\)
AH=4*3/5=2,4cm
b: ΔCAD cân tại C
mà CH là đường cao
nên CH là phân giác của góc ACD
Xét ΔCAB và ΔCDB có
CA=CD
góc ACB=góc DCB
CB chung
Do dó: ΔCAB=ΔCDB
=>góc CDB=90 độ
=>BD là tiếp tuyến của (C)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, đường cao AH, có AB =6cm, BH =3cm. Tia AH cắt đường tròn ngoại tiếp tam giác ABC tại D, CA cắt DB tại E. so sánh BE và BC
Cho tam giác ABC vuông tại A (AB < AC), đường cao AH vẽ đường tròn tâm B bán kính ba, lấy điểm D thuộc đường tròn nằm trong tam giác ABC, tia CD cắt đường cao AH tại F và cắt đường tròn (B) tại E, qua điểm D vẽ đường thằng song song với AE cắt ah tại N và AC. Chứng minh:
1. Góc ABD = 2 lần góc MDC
2. CD.CD = CA^2
2: Xét ΔCAD và ΔCEA có
góc C chung
góc CAD=góc CEA
=>ΔCAD đồng dạng với ΔCEA
=>CA/CE=CD/CA
=>CA^2=CE*CD
Đúng 0
Bình luận (0)
Câu 4: Cho tam giác ABC vuông tại A (AB AC), có đường cao AH.1. Cho AB 4cm; AC 3cm. Tính độ dài các đoạn thẳng BC, AH.2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D. a) Chứng minh BD là tiếp tuyến của đường tròn (C). b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Chứng minh: 2 PE.QF EF
Đọc tiếp
Câu 4: Cho tam giác ABC vuông tại A (AB > AC), có đường cao AH.
1. Cho AB = 4cm; AC = 3cm. Tính độ dài các đoạn thẳng BC, AH.
2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D.
a) Chứng minh BD là tiếp tuyến của đường tròn (C).
b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Chứng minh: 2 PE.QF = EF
Câu 4: Cho tam giác ABC vuông tại A (AB AC), có đường cao AH. 1. Cho AB 4cm; AC 3cm. Tính độ dài các đoạn thẳng BC, AH. 2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D. a) Chứng minh BD là tiếp tuyến của đường tròn (C). b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Chứng minh: 2 PE.QF EF
Đọc tiếp
Câu 4: Cho tam giác ABC vuông tại A (AB > AC), có đường cao AH. 1. Cho AB = 4cm; AC = 3cm. Tính độ dài các đoạn thẳng BC, AH. 2. Vẽ đường tròn tâm C, bán kính CA. Đường thẳng AH cắt đường tròn (C) tại điểm thứ hai D. a) Chứng minh BD là tiếp tuyến của đường tròn (C). b) Qua C kẻ đường thẳng vuông góc với BC cắt các tia BA, BD thứ tự tại E, F. Trên cung nhỏ AD của (C) lấy điểm M bất kỳ, qua M kẻ tiếp tuyến với (C) cắt AB, BD lần lượt tại P, Q. Chứng minh: 2 PE.QF = EF
Cho tam giác \(ABC\) vuông tại \(A\) có \(AB = 3cm,AC = 4cm.\) Đường phân giác của góc \(A\) cắt \(BC\) tại \(D\).
a) Tính \(BC,BD,DC\).
b) Vẽ đường cao \(AH\). Tính \(AH,HD\) và \(AD\).
a)
Xét tam giác \(ABC\) vuông tại \(A\) ta có:
\(A{B^2} + A{C^2} = B{C^2}\)
\( \Leftrightarrow {3^2} + {4^2} = B{C^2}\)
\( \Leftrightarrow B{C^2} = 25\)
\( \Rightarrow BC = 5cm\)
Ta có: \(BD + DC = BC \Rightarrow DC = BC - BD = 5 - BD\)
Vì \(AD\) là phân giác của góc \(BAC\) nên theo tính chất đường phân giác ta có:
\(\frac{{BD}}{{DC}} = \frac{{AB}}{{AC}} \Leftrightarrow \frac{{BD}}{{5 - BD}} = \frac{3}{4} \Leftrightarrow 4.BD = 3.\left( {5 - BD} \right) \Rightarrow 4.BD = 15 - 3.BD\)
\( \Leftrightarrow 4BD + 3BD = 15 \Leftrightarrow 7BD = 15 \Rightarrow BD = \frac{{15}}{7}\)
\( \Rightarrow DC = 5 - \frac{{15}}{7} = \frac{{20}}{7}\)
Vậy \(BC = 5cm;BD = \frac{{15}}{7}cm;DC = \frac{{20}}{7}cm\).
b) Diện tích tam giác \(ABC\) vuông tại \(A\) là:
\({S_{ABC}} = \frac{1}{2}AB.AC = \frac{1}{2}.4.3 = 6\left( {c{m^2}} \right)\)
Mặt khác \({S_{ABC}} = \frac{1}{2}.AH.BC = \frac{1}{2}.AH.5 = 6\)
\( \Rightarrow AH = \frac{{6.2}}{5} = 2,4cm\).
Xét tam giác \(AHB\) vuông tại \(H\) ta có:
\(A{H^2} + H{B^2} = A{B^2}\)
\( \Leftrightarrow H{B^2} = A{B^2} - A{H^2}\)
\( \Leftrightarrow H{B^2} = {3^2} - 2,{4^2}\)
\( \Leftrightarrow H{B^2} = 3,24\)
\( \Rightarrow HB = 1,8cm\)
\(HD = BD - BH = \frac{{15}}{7} - 1,8 = \frac{{12}}{7}cm\).
Xét tam giác \(AHD\) vuông tại \(H\) ta có:
\(A{H^2} + H{D^2} = A{D^2}\)
\( \Leftrightarrow A{D^2} = {\left( {\frac{{12}}{7}} \right)^2} + 2,{4^2}\)
\( \Leftrightarrow A{D^2} = \frac{{144}}{{49}} + \frac{{144}}{{25}}\)
\( \Rightarrow AD \approx 2,95cm\)
Vậy \(AH = 2,4cm;HD = \frac{{12}}{7}cm;AD = 2,95cm\).
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A có AB = 4cm; AC = 3cm. Tính diện tích của tam giác ABC và đường cao AH. (vẽ hình C/M giúp)
Xem chi tiết
Hình vẽ bạn phải tự vẽ được chứ, bài này là bài rất rất rất cơ bản rồi đấy:vv
Ta có tam giác ABC là tam giác vuông
=> SABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.4.3=6\) (cm2)
Áp dụng định lý Py-ta-go vào tam giác vuông ABC:
BC2=AB2+AC2=42+32=52
=> BC=5(cm)
Mà SABC=\(\dfrac{1}{2}.AH.BC=\dfrac{1}{2}.AH.5=2,5.AH=6\)
=> AH=2,4(cm)
Vậy...
Có thể do cẩu thả mình sai số chỗ nào đó nhưng hướng làm như này nhé, đáng nhẽ bài này mình không giải đâu:vv
Đúng 2
Bình luận (1)
Cho tam giác ABC vuông tại A có AB = 4cm; AC = 3cm. Tính diện tích của tam giác ABC và đường cao AH. (vẽ hình C/M giúp)
plz
Xem chi tiết
Cho tam giác ABC vuông tại A có đường cao AH. Vẽ đường tròn tâm A, bán kính AH.Đường tròn đường kính BC cắt đường tròn (A) tại M và N, MN cắt AH tại I. CM: I là trung điểm của AH.













