Ta có: \(\dfrac{5}{-x^2+5x-6}+\dfrac{x+3}{2-x}=0\)

\(\Leftrightarrow\dfrac{-5}{\left(x-2\right)\left(x-3\right)}-\dfrac{x^2-9}{\left(x-2\right)\left(x-3\right)}=0\)

\(\Leftrightarrow-5-x^2+9=0\)

\(\Leftrightarrow x=-2\)

Đáp án: D

2 - x = x  nên x > 0 kết hợp đkxđ x ≤ 2  khi đó phương trình có nghiệm thỏa mãn  0 < x ≤ 2   ⇒ a sai.

7 - 4 3 = 2 - 3 . ⇒ b sai

2 x - 1 x - 2 = x + 1 x - 2 ⇒ 2x – 1 = x + 1 ( x ≠ 2 ) ⇔ x = 2 (loại).

Vậy phương trình vô nghiệm. ⇒ c đúng.

  5 x 2 - 4 5 x + 3 < - 1 ⇔ 5 x 2 - 4 5 x + 4 < 0 ⇔ 5 x - 2 2 < 0 (vô lí) ⇒ d sai.

 có 1 mệnh đề đúng.

Lời giải:

$\Delta'=(\sqrt{3}-1)^2+4\sqrt{3}=(\sqrt{3}+1)^2$
Do đó pt có 2 nghiệm:
\(x_1=\frac{-b'+\sqrt{\Delta'}}{a}=\frac{1-\sqrt{3}+\sqrt{3}+1}{\sqrt{3}}=\frac{2}{\sqrt{3}}\)

\(x_2=\frac{-b'-\sqrt{\Delta'}}{a}=\frac{1-\sqrt{3}-\sqrt{3}-1}{\sqrt{3}}=-2\)

1/ \(7x-5=13-5x\)

\(\Leftrightarrow12x=18\)

\(\Leftrightarrow x=\dfrac{3}{2}\)

Vậy: \(S=\left\{\dfrac{3}{2}\right\}\)

==========

2/ \(19+3x=5-18x\)

\(\Leftrightarrow21x=-14\)

\(\Leftrightarrow x=-\dfrac{2}{3}\)

Vậy: \(S=\left\{-\dfrac{2}{3}\right\}\)

==========

3/ \(x^2+2x-4=-12+3x+x^2\)

\(\Leftrightarrow-x=-8\)

\(\Leftrightarrow x=8\)

Vậy: \(S=\left\{8\right\}\)

===========

4/ \(-\left(x+5\right)=3\left(x-5\right)\)

\(\Leftrightarrow-x-5=3x-15\)

\(\Leftrightarrow-4x=-10\)

\(\Leftrightarrow x=\dfrac{5}{2}\)

Vậy: \(S=\left\{\dfrac{5}{2}\right\}\)

==========

5/ \(3\left(x+4\right)=\left(-x+4\right)\)

\(\Leftrightarrow3x+12=-x+4\)

\(\Leftrightarrow4x=-8\)

\(\Leftrightarrow x=-2\)

Vậy: \(S=\left\{-2\right\}\)

[----------]

1. \(7x-5=13-5x\) \(\Leftrightarrow12x=18\Leftrightarrow x=\dfrac{3}{2}\)

2. \(19+3x=5-18x\Leftrightarrow21x=-14\Leftrightarrow x=-\dfrac{2}{3}\)

3. \(x^2+2x-4=-12+3x+x^2\Leftrightarrow-x=-8\Leftrightarrow x=8\)

4. \(-\left(x+5\right)=3\left(x-5\right)\Leftrightarrow-x-5=3x-15\Leftrightarrow4x=10\Leftrightarrow x=\dfrac{5}{2}\)

5. \(3\left(x+4\right)=-x+4\Leftrightarrow3x+12=-x+4\Leftrightarrow4x=-8\Leftrightarrow x=-2\)

1) Ta có: \(7x-5=13-5x\)

\(\Leftrightarrow12x=18\)

hay \(x=\dfrac{3}{2}\)

2) Ta có: \(19+3x=5-18x\)

\(\Leftrightarrow21x=-14\)

hay \(x=-\dfrac{2}{3}\)

3) Ta có: \(x^2+2x-4=x^2+3x-12\)

\(\Leftrightarrow3x-12=2x-4\)

hay x=8

4) Ta có: \(-\left(x+5\right)=3\left(x-5\right)\)

\(\Leftrightarrow-x-5-3x+15=0\)

\(\Leftrightarrow-4x=-10\)

hay \(x=\dfrac{5}{2}\)

Bạn xem lại đề

Dưới căn là \(\sqrt{2x^2+1}\) hay \(\sqrt{2x^2-1}\)

b) 5x(x-2000)-x+2000=0

\(\Rightarrow5x\left(x-2000\right)-\left(x-2000\right)=0\\ \Rightarrow\left(x-2000\right)\left(5x-1\right)=0\)

\(\Rightarrow\left\{{}\begin{matrix}x-2000=0\\5x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0+2000\\5x=0+1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\5x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2000\\x=\dfrac{1}{5}\end{matrix}\right.\)

Ai giúp minh làm bài 5 phía trên với

c) Ta có: \(2x\left(x-2\right)+3\left(x-2\right)=0\)

\(\Leftrightarrow\left(x-2\right)\left(2x+3\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{-3}{2}\end{matrix}\right.\)

d) Ta có: \(5x^2+x=0\)

\(\Leftrightarrow x\left(5x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{-1}{5}\end{matrix}\right.\)

a)

5 x 2 − 3 x + 1 = 2 x + 11 ⇔ 5 x 2 − 3 x + 1 − 2 x − 11 = 0 ⇔ 5 x 2 − 5 x − 10 = 0

Có a = 5; b = -5; c = -10 ⇒ a - b + c = 0

⇒ Phương trình có hai nghiệm:  x 1   =   - 1   v à   x 2   =   - c / a   =   2 .

Vậy phương trình có tập nghiệm S = {-1; 2}.

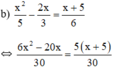
⇔ 6 x 2 − 20 x = 5 ( x + 5 ) ⇔ 6 x 2 − 20 x − 5 x − 25 = 0 ⇔ 6 x 2 − 25 x − 25 = 0

Có a = 6; b = -25; c = -25

⇒   Δ   =   ( - 25 ) 2   –   4 . 6 . ( - 25 )   =   1225   >   0

⇒ Phương trình có hai nghiệm

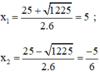
Vậy phương trình có tập nghiệm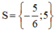 

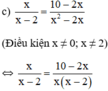
⇔ x 2 = 10 − 2 x ⇔ x 2 + 2 x − 10 = 0

Có a = 1; b = 2; c = -10  ⇒   Δ ’   =   1 2   –   1 . ( - 10 )   =   11   >   0

⇒ Phương trình có hai nghiệm

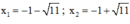
Cả hai nghiệm đều thỏa mãn điều kiện xác định.

Vậy phương trình có tập nghiệm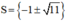 

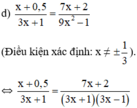
⇔ ( x + 0 , 5 ) ⋅ ( 3 x − 1 ) = 7 x + 2 ⇔ 3 x 2 + 1 , 5 x − x − 0 , 5 = 7 x + 2 ⇔ 3 x 2 − 6 , 5 x − 2 , 5 = 0

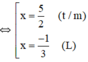
Vậy phương trình có tập nghiệm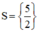 

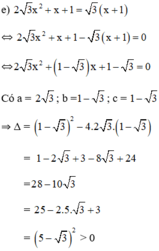
⇒ Phương trình có hai nghiệm

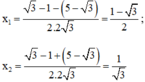
Vậy phương trình có tập nghiệm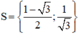 

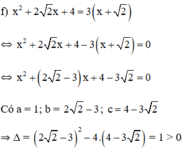
Phương trình có hai nghiệm:

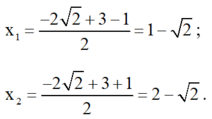
Vậy phương trình có tập nghiệm 

 x⁴+2x³-2x²+2x-3=0

=>  (x⁴ - 1) + (2x³-2x² )+ (2x-2)=0

=> (x - 1).(x+1).(x² + 1) + 2x².(x - 1) + 2.(x -1) = 0

=> (x -1). [(x+1).(x² + 1) + 2x² + 2] = 0

<=> (x - 1). (x³ + x + x² + 1 + 2x² + 2)= 0

<=> (x - 1). (x³ + x + 3x² + 3)= 0

<=> x - 1 = 0 hoặc x³ + x + 3x² + 3 = 0

+) x - 1 = 0 => x  =1 

+) x³ + x + 3x² + 3 = 0 <=> x. (x² + 1) + 3.(x² + 1) = 0

<=> (x+3). (x² +1) = 0 <=> x + 3 = 0 (vì x² + 1 > 0 với mọi x)

<=> x = -3

Vậy pt có 2 nghiệm x = 1 ; x = -3

X^4+2X^3-X^2+2X+1=0 LAM TN

(x^4+x^3+x+1)/(x^4-x^3+2x^2-x+1)>=0