cho tam giác abc cân tại a a 75 độ tính số đo góc bc

Những câu hỏi liên quan
Cho tam giác ABC có góc A=75 độ ,B=35 độ .Phân giác của góc BAC cắt cạnh BC tại D.Đường thẳng qua A vuông góc với AD cắt tia BC tại E.Gọi M là trung điểm của DE:
a/Tính số đo góc MAE
b/Chứng minh rằng tam giác ACM là tam giác cân.
Cho tam giác ABC có góc A = 75 độ. Lấy điểm D trên cạnh BC sao cho tam giác ABD và tam giác ACD là tam giác cân. Tính số đo 2 góc còn lại của tam giác ABC.
cho tam giác ABC cân tại A , B = 30 độ kẻ AH vuông góc BC ( H thuộc BC ) tính số đo góc A
\(\Delta ABC\text{cân tại A }:\)
\(\Leftrightarrow\widehat{B}=\widehat{C}=30^0\)
\(TC:\)
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
\(\Rightarrow\widehat{A}=180^0-2\widehat{B}=180-2\cdot30^0=120^0\)
Đúng 4
Bình luận (0)
Cho tam giác ABC , góc A = 75o .Điểm D nằm trên cạnh BC sao cho tam giác ABD và tam giác ACD cân ( không bắt buộc cân tại đâu ) .Tính số đo 2 góc còn lại của tam giác ABC .
( Lưu ý : hình chỉ mang tính minh họa )
Chứng minh
Ta thấy cả 2 tam giác ABD và tam giác ACD không thể cùng cân ở A ( vì AB=AD=AC, nên B,D,C nằm trên một đường tròn tâm A bán kính AB do đó B,C,D không thẳng hàng ).
Nếu cả hai tam giác ABD và ACD cùng cân ở D thì tam giác ABC sẽ vuông ở A ( Mâu thuẫn với giả thiết \(\widehat{A}\)= 750 )
Nếu tam giác ABD cân ở B thì AB=BD , tam giác ACD cân ở C thì AC=CD khi đó AB+AC=BD+DC hay AB+AC=BC ( vô lý vì trong 1 tam giác thì tổng 2 cạnh lớn hơn 1 cạnh )
Vì vậy tam giác ABD sẽ cân ở A và tam giác ACD phải cân ở D
Vì tam giác ABD cân ở A nên \(\widehat{B}=\widehat{D1}\left(tinhchat\right)\)
Vì tam giác ACD cân ở D nên \(\widehat{A1}=\widehat{C}\left(tinhchat\right)\)
Ta có \(\widehat{D1}\)là góc ngoài của tam giác ABC tại D
\(\Rightarrow\widehat{D1}=\widehat{A1}+\widehat{C}\left(tinhchat\right)\)mà \(\widehat{A1}=\widehat{C}\left(cmt\right)\)
\(\Rightarrow\widehat{D1}=2.\widehat{A1}\)mà \(\widehat{B}=\widehat{D1}\left(cmt\right)\)
\(\Rightarrow\widehat{B}=2.\widehat{A1}\)
Ta có: \(\widehat{A}+\widehat{B}+\widehat{C}=\widehat{A1}+\widehat{A2}+\widehat{A1}+2.\widehat{A1}\)
\(180^0=4.\widehat{A1}+\widehat{A2}\)(1)
Lại có : \(\widehat{A1}+\widehat{A2}=75^0\)(2)
Lấy (1) trừ (2) ta được: \(3.\widehat{A1}=105^0\)
\(\widehat{A1}=35^0\)
\(\Rightarrow\widehat{C}=35^0\)( vì \(\widehat{C}=\widehat{A1}\))
Xét tam giác ABC có: \(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)( định lý )
\(\widehat{B}=70^0\)
Vậy ...
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho tam giác ABC cân tại A có góc BAC = 100 độ . Lấy D thuộc BC sao chô góc DAC = 20 độ , trên tia AD lấy E sao cho tam giác ACE cân tại C . Tính số đo các góc trong tam giác BDE .
cô ơi trong tuồn nay làm hết toán ,tiếng việt ,tiếng anh phải không cô
lộn đề ak nguyễn thị phương giang
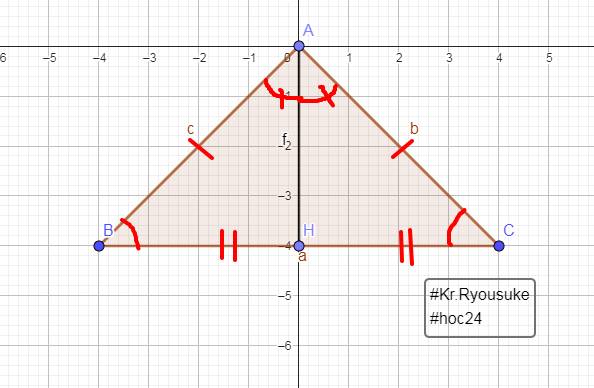
cho tam giác ABC cân tại A, đường cao AH (H thuộc BC)
a. tam giác AHB có bằng tam giác AHC không?vì sao?
b. cho góc BAH có số đo bằng 35 độ. tính số đo góc CAH?
c. cho BH=4cm. tính độ dài đoạn thẳng CH?
`a,`
Vì `\Delta ABC` cân tại A:
`-> \text {AB = AC, }` $\widehat {B} = \widehat {C}$.
Xét `\Delta AHB` và `\Delta AHC` :
`\text {AB = AC}`
$\widehat {B} = \widehat {C}$
$\widehat {AHB} = \widehat {AHC} (=90^0) (\text {AH là đường cao})$
`=> \Delta AHB = \Delta AHC (ch-gn)`
`b,`
Vì `\Delta AHB = \Delta AHC (a)`
`->` $\widehat {BAH} = \widehat {CAH} (\text {2 góc tương ứng})$
Mà $\widehat {BAH} = 35^0$
`->` $\widehat {BAH} = \widehat {CAH} = 35^0.$
`c,`
`\Delta AHB = \Delta AHC (a)`
`-> \text {BH = CH (2 cạnh tương ứng)}`
Mà `\text {BH = 4 cm}`
`-> \text {BH = CH = 4 cm}`
Đúng 3
Bình luận (0)
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có
AB=AC
AH chung
=>ΔAHB=ΔAHC
b: góc CAH=góc BAH=35 độ
c: HC=HB=4cm
Đúng 1
Bình luận (0)
1.Cho tam giác ABC cân tại B. trên AB,BC lần lượt lấy M,N sao cho AICK. có góc BCA42 độ. số đo góc KIA là...độ2.Cho tam giác ABC cân tại A có góc A112 độ. Trên AB,AC lần lượt lấy M,N sao cho AMAN. Số đo góc MNC là...độ3.Cho tam giác ABC cân tại A có góc A78 độ. Gọi E,F lần lượt là trung điểm AB,AC. Có góc BCE26 độ. Số đo góc AFB là...độ4.Cho tam giác ABC cân tại A. Gọi M,N lần lượt là trung điểm AB,AC. Cho góc BAC84 độ, gócABN30 độ. Số đo góc BCM là...độ
Đọc tiếp
1.Cho tam giác ABC cân tại B. trên AB,BC lần lượt lấy M,N sao cho AI=CK. có góc BCA=42 độ. số đo góc KIA là...độ
2.Cho tam giác ABC cân tại A có góc A=112 độ. Trên AB,AC lần lượt lấy M,N sao cho AM=AN. Số đo góc MNC là...độ
3.Cho tam giác ABC cân tại A có góc A=78 độ. Gọi E,F lần lượt là trung điểm AB,AC. Có góc BCE=26 độ. Số đo góc AFB là...độ
4.Cho tam giác ABC cân tại A. Gọi M,N lần lượt là trung điểm AB,AC. Cho góc BAC=84 độ, gócABN=30 độ. Số đo góc BCM là...độ
Cho tam giác cân ABC cân tại A, góc A =100 độ .Trên tia đối của tia BA lấy điểm D sao cho AD = BC. Tính số đo góc ADC
Cho tam giác ABC cân tại A
a) Biết B=55 độ, tính số đo góc A
b) Cho M là trung điểm của BC. Chứng minh AM vuông góc với BC
a) vì ΔABC cân tại A nên ta có :
\(\widehat{B}=\widehat{C}\) (2 góc đáy của ΔABC cân tại A)
ta có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\) (tổng số đo ba góc trong 1 tam giác)
\(\Rightarrow\widehat{A}+55^o+55^o=180^o\)
\(\Rightarrow\widehat{A}=180^o-55^o-55^o=70^o\)
vậy \(\widehat{A}\) có số đo là 70o
b) xét ΔAMB và ΔAMC, ta có :
AB = AC (2 cạnh bên của ΔABC cân tại A)
MB = MC (vì M là trung điểm của BC)
AM là cạnh chung
⇒ ΔAMB = ΔAMC (c.c.c)
⇒ \(\widehat{AMB}=\widehat{AMC}\) (2 góc tương ứng)
ta có : \(\widehat{AMB}+\widehat{AMC}=180^o\) (kề bù)
\(\Rightarrow\widehat{AMB}=\widehat{AMC}=\dfrac{180^o}{2}=90^o\)
⇒ AM ⊥ BC
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A và góc A = 100 độ. Trên tia AC lấy D sao cho AD = BC. Tính số đo góc CBD.




















