a: Gọi E là trung điểm của BC

=>A,G,E thẳng hàng và AG=2GE

Xét ΔEABcó GM//AB

nên BM/BE=AG/AE=2/3

=>BM=2/3BE=2/3*1/2BC=1/3BC

b: Xét ΔEAC có GN//AC
nên CN/CE=AG/AE=2/3

=>CN=2/3*CE=2/3*1/2BC=1/3BC

MN=BC-BM-CN=1/3BC

=>BM=MN=NC

Lời giải:

Lấy \(BG\cap AC\equiv E; CG\cap AB\equiv F\)

Vì $G$ là trọng tâm tam giác $ABC$ nên \(\frac{BG}{BE}=\frac{CG}{CF}=\frac{2}{3}\)

Xét tam giác $BEC$ có \(GN\parallel EC\Rightarrow \frac{BN}{BC}=\frac{BG}{BE}=\frac{2}{3}\) (định lý Thales)

\(\Leftrightarrow \frac{BC-BN}{BC}=\frac{1}{3}\Leftrightarrow \frac{NC}{BC}=\frac{1}{3}\) (1)

Xét tam giác $CFB$ có \(GM\parallel FB\Rightarrow \frac{MC}{CB}=\frac{GC}{CF}=\frac{2}{3}\) (định lý Thales)

\(\Leftrightarrow \frac{CB-MC}{CB}=\frac{1}{3}\Leftrightarrow \frac{MB}{CB}=\frac{1}{3}\) (2)

Từ (1); (2)

\(\Rightarrow MN=BC-NC-MB=BC-\frac{1}{3}BC-\frac{1}{3}BC=\frac{1}{3}BC\)

Do đó: \(BM=MN=NC(=\frac{BC}{3})\)

Ta có đpcm.

a: Xét tứ giác BMNC có MN//BC

nên BMNC là hình thang

mà \(\widehat{B}=\widehat{C}\)

nên BMNC là hình thang cân

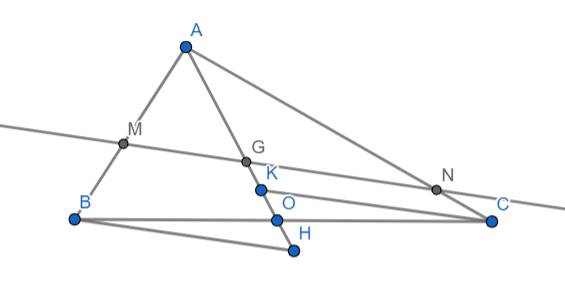
Xét 2 tam giác AMG và ABH ta có:

\(\widehat{BAH}\) chung 

\(\widehat{AMG}=\widehat{ABH}\) (cặp góc đồng vị do BH//MG) 

\(\Rightarrow\Delta AMG\sim\Delta ABH\left(g.g\right)\) 

\(\Rightarrow\dfrac{AB}{AM}=\dfrac{AH}{AG}\) (1) 

Xét 2 tam giác ANG và ACK có:

\(\widehat{CAK}\) chung 

\(\widehat{ANG}=\widehat{ACK}\) (cặp góc đồng vị do CK//GN) 

\(\Rightarrow\Delta ANG\sim\Delta ACK\left(g.g\right)\)

\(\Rightarrow\dfrac{AC}{AN}=\dfrac{AK}{AG}\) (2) 

Xét hai tam giác BOH và COK ta có: 

\(\widehat{BOH}=\widehat{COK}\) (đối đỉnh) 

\(BO=CO\) (AO là đường trung tuyến nên O là trung điểm của BC) 

\(\widehat{HBO}=\widehat{KCO}\) (so le trong vì BH//MN và CK//MN ⇒ BH//CK) 

\(\Rightarrow\Delta BOH=\Delta COK\left(g.c.g\right)\) 

\(\Rightarrow HO=OK\) (hai cạnh t.ứng) 

\(\Rightarrow HK=2HO\)

Ta lấy (1) + (2) \(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{AH+AK}{AG}=\dfrac{AH+AH+HK}{AG}=\dfrac{2AH+HK}{AG}\) 

\(=\dfrac{2AH+2HO}{AG}=\dfrac{2\left(AH+HO\right)}{AG}=\dfrac{2AO}{AG}\) 

Mà G là trọng tâm của tam giác ABC \(\Rightarrow AO=\dfrac{3}{2}AG\) 

\(\Rightarrow\dfrac{AB}{AM}+\dfrac{AC}{AN}=\dfrac{2\cdot\dfrac{3}{2}AG}{AG}=2\cdot\dfrac{3}{2}=3\left(đpcm\right)\)  

T/g BMN đồng dạng vs t/g BAC theo tỉ số 2/3 => C(BMN) = 2/3 C(BAC) = 50cm

\(\frac{MB}{AB}=\frac{2}{3}\Rightarrow\frac{MB}{AB-MB}=\frac{MB}{AM}=\frac{2}{3-2}=2\Rightarrow MB=2AM\)

tương tự, BN=2NC

MN = C(BMN) - BM - BN = 50 - 2(AM+NC) = 18cm