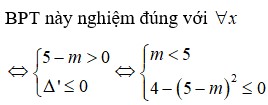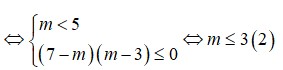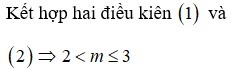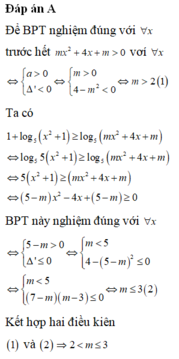Tìm các giá trị của tham số m để bất phương trình mx2-(2m-1)x +1<0 có tập nghiệm là (-∞;+∞)

Những câu hỏi liên quan
Tìm các giá trị của tham số m để bất phương trình
m
x
2
-
(
2
m
-
1
)
x
+
1
0
Đọc tiếp
Tìm các giá trị của tham số m để bất phương trình m x 2 - ( 2 m - 1 ) x + 1 < 0

Số giá trị nguyên của tham số m ∈ (-10;10) để bất phương trình mx2 -2mx-1+2m≤0 với mọi x∈R
\(mx^2-2mx-1+2m< =0\)(1)
TH1: m=0
BPT (1) sẽ trở thành
\(0\cdot x^2-2\cdot0\cdot x-1-2\cdot0< =0\)
=>-1<=0(luôn đúng)
=>Nhận
TH2: m<>0
\(\text{Δ}=\left(-2m\right)^2-4\cdot m\cdot\left(2m-1\right)\)
\(=4m^2-8m^2+4m=-4m^2+4m\)
Để BPT (1) luôn đúng với mọi x thuộc R thì
\(\left\{{}\begin{matrix}\text{Δ}< =0\\a< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4m^2+4m< =0\\m< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-4m\left(m-1\right)< =0\\m< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}m\left(m-1\right)>=0\\m< 0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}m>=1\\m< =0\end{matrix}\right.\\m< 0\end{matrix}\right.\)
=>m<0
Do đó: m<=0
mà \(m\in Z;m\in\left(-10;10\right)\)
nên \(m\in\left\{-9;-8;...;-1;0\right\}\)
=>Số giá trị nguyên thỏa mãn là 10
Đúng 1
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m để bất phương trình
1
+
log
5
(
x
2
+
1
)
≥
log
5
(
m
x
2
+
4
x
+
m
)
có nghiệm đúng
∀
x
A.
m
∈
(
2
;
...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log 5 ( x 2 + 1 ) ≥ log 5 ( m x 2 + 4 x + m ) có nghiệm đúng ∀ x
A. m ∈ ( 2 ; 3 ]
B. m ∈ ( - 2 ; 3 ]
C. m ∈ [ 2 ; 3 )
D. m ∈ [ - 2 ; 3 )
Tìm tất cả các giá trị thực của tham số m để bất phương trình
1
+
log
5
(
x
2
+
1
)
≥
log
5
(
m
x
2
+
4
x
+
m
)
có nghiệm đúng
∀
x
A.
m
∈
(...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình 1 + log 5 ( x 2 + 1 ) ≥ log 5 ( m x 2 + 4 x + m ) có nghiệm đúng ∀ x
A. m ∈ ( 2 ; 3 ]
B. m ∈ ( - 2 ; 3 ]
C. m ∈ [ 2 ; 3 )
D. m ∈ [ - 2 ; 3 )
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình:
x
2
-
3
x
+
2
≤
0
cũng là nghiệm của bất phương trình
m
x
2
+
(
m
+
1
)
x
+
m
+
1
≥
0
? A.
m
≤
-
1
. B....
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x 2 - 3 x + 2 ≤ 0 cũng là nghiệm của bất phương trình m x 2 + ( m + 1 ) x + m + 1 ≥ 0 ?
A. m ≤ - 1 .
B. m ≤ - 4 7 .
C. m ≥ - 4 7 .
D. m ≥ - 1 .
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2
≤
0
cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1
≥
0
A.
m
≤
-
1
B.
m
≤
-
4
7
C.
m
≥
-
4
7
D.
m
≥
-
1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2-3x+2 ≤ 0 cũng là nghiệm của bất phương trình mx2+(m+1) x+m+1 ≥ 0
A. m ≤ - 1
B. m ≤ - 4 7
C. m ≥ - 4 7
D. m ≥ - 1
Bất phương trình x2-3x+2 ≤ 0 ⇔ 1 ≤ x ≤ 2
Bất phương trình mx2+(m+1) x+m+1 ≥ 0
![]()
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 , 1 ≤ x ≤ 2
Có f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx2+ (m+ 1) x+ m+1≥0? A. m -1 B.
m
≤
-
4
7
. C.
m
≥
-
4
7
. D. m -1
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho mọi nghiệm của bất phương trình: x2- 3x+ 2≤ 0 cũng là nghiệm của bất phương trình mx2+ (m+ 1) x+ m+1≥0?
A. m< -1
B. m ≤ - 4 7 .
C. m ≥ - 4 7 .
D. m> -1
Giải bất phương trình x2- 3x+ 2≤ 0 ta được 1≤x≤2.
Bất phương trình mx2+ (m+ 1) x+ m+1≥0
⇔ m ( x 2 + x + 1 ) ≥ - x - 2 ⇔ m ≥ - x - 2 x 2 + x + 1
Xét hàm số f ( x ) = - x - 2 x 2 + x + 1 với 1≤ x≤ 2
Có đạo hàm f ' ( x ) = x 2 + 4 x + 1 ( x 2 + x + 1 ) 2 > 0 , ∀ x ∈ 1 ; 2
Yêu cầu bài toán ⇔ m ≥ m a x [ 1 ; 2 ] f ( x ) ⇔ m ≥ - 4 7
Chọn C.
Đúng 0
Bình luận (0)
Tìm các giá trị của tham số m để mọi giá trị của x nhỏ hơn \(\dfrac{-1}{2}\) đều là nghiệm của bất phương trình (2m + 3).(x - m) > 4x - 3 + 2m
Tìm các giá trị của tham số m để phương trình
m
x
2
+
2
(
2
m
-
1
)
x
+
m
+
2
0
vô nghiệm A.
3
-
6
3
m...
Đọc tiếp
Tìm các giá trị của tham số m để phương trình m x 2 + 2 ( 2 m - 1 ) x + m + 2 = 0 vô nghiệm
A. 3 - 6 3 < m < 3 + 6 3
B. Không tồn tại m
C. m < 1/12
D. m ≠ 0; m < 1/12
Tìm tổng các giá trị thực của tham số m để phương trình mx2 - 2mx - 2m - 1 = 0 có 2 nghiệm phân biệt x1; x2
thỏa mãn
x12 + 2x1x2 + 3x22 = 4x1 + 5x2 - 1
Lời giải:
PT có 2 nghiệm pb khi:
$\Delta'=m^2+m(2m+1)>0\Leftrightarrow m(3m+1)>0\Leftrightarrow m>0$ hoặc $m< \frac{-1}{3}(*)$
Theo định lý Viet: \(\left\{\begin{matrix} x_1+x_2=2\\ x_1x_2=\frac{-(2m+1)}{m}\end{matrix}\right.\) . Khi đó:
$x_1^2+2x_1x_2^2+3x_2^2=4x_1+5x_2-1$
$\Leftrightarrow (x_1+x_2)^2+2x_2^2=4(x_1+x_2)+x_2-1$
$\Leftrightarrow 4+2x_2^2=7+x_2$
$\Leftrightarrow 2x_2^2-x_2-3=0$
$\Leftrightarrow x_2=\frac{3}{2}$ hoặc $x_2=-1$
$x_2=\frac{3}{2}$ thì $x_1=\frac{1}{2}$
$\frac{-(2m+1)}{m}=x_1x_2=\frac{3}{4}\Leftrightarrow m=\frac{-4}{11}$
$x_2=-1$ thì $x_1=3$
$\frac{-(2m+1)}{m}=x_1x_2=-3\Leftrightarrow m=1$
(hai giá trị trên đều thỏa mãn)
Đúng 1
Bình luận (1)