tính giá trị biểu thức A=x^15-8x^14+8x^13-8x^12+...-8x^2+8x-5 với x=7
Tính giá trị của biểu thức sau: A=4x-5y/8x-7y. a) Tại x=-2, y=3; b) Biết x/y=5/4
a, Thay x = -2 ; y = 3 ta được
\(A=\dfrac{4\left(-2\right)-5.3}{8\left(-2\right)-7.3}=\dfrac{-8-15}{-16-21}=\dfrac{23}{37}\)
b, Ta có \(\dfrac{x}{y}=\dfrac{5}{4}\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=k\Rightarrow x=5k;y=4k\)
Thay vào ta được \(A=\dfrac{4.5k-5.4k}{8.5k-7.4k}=\dfrac{0}{40k-28k}=0\)
Tính giá trị biểu thức
1/8x³ - 3/2x²+ 6x- 8x tại x=24
\(=\dfrac{1}{8}\cdot24^3-\dfrac{3}{2}\cdot24^2-2\cdot24=816\)
Tính giá trị của biểu thức sau: x= -1,y=2
A: 5+2.(8x+2)
B:2.(y^2 - 4x)
Với x=-1 giá trị biểu thức A là
5+2.[8.(-1)+2]=5+2.(-8+2)=5+2.(-6)=5-12= -7
Với x=-1; y=2 giá trị biểu thức B là
2.(y2-4x)=2.[22-4.(-1)]=2.(4+4)=2.8=16
a) Thay x vào biểu thức 5+2.(8x+2)
Ta được : 5 + 2. ( 8.(-1)+2)
= 5 + 2. (-6)
= 5 + ( -4 )
= 1
b) Thay x = -1 và y = 2 vào biểu thức 2.(\(y^2-4x\))
Ta được : \(2.\left(2^2-4.\left(-1\right)\right)\)
= 2. [ 4 - 4 . ( -1 )]
= 2. 0
= 0
Với mọi giá trị của x thì giá trị của biểu thức 2x(3x−1)−6x(x+1)+(3+8x) là: *
AMột đáp số khác
B2
C3
D4
Cho z = x + y i với x, y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ | z + i - 2 | ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 x . Tính M+m.
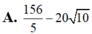
![]()
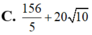
![]()
A = x^15-8x^14+8x^13-8x^12+⋯-8x^2+8x-5 với x = 7
x=7
nên x+1=8
\(A=x^{15}-x^{14}\left(x+1\right)+x^{13}\left(x+1\right)-...-x^2\left(x+1\right)+x\left(x+1\right)-5\)
\(=x-5=7-5=2\)
Chứng minh rằng các biểu thức sau luôn nhận giá trị âm với mọi giá trị của biến
R=-x2-y2+8x+4y-21
-(x2-8x+16)-(y2-4y+4)= -(x-4)2-(y-2)2
Ta có : -(x-4)2<= 0
suy ra: -(x-4)2-(y-2)2<=0 (dpcm)
![]()
Tính giá trị biểu thức B = y3 + 4x2y + 4xy + 8x3 + 2xy2 với 2xy = 1
tính giá trị biểu thức A= x^15 - 8x^14 + 8x^13 - 8x^12 +....- 8x^2 + 8x - 5 Với x=7
x=7
=>x+1=8
=> A= x^15 - 8x^14 + 8x^13 - 8x^12 +....- 8x^2 + 8x - 5
=x15-(x+1)x14+(x+1)x13-(x+1)x12+...-(x+1)x2+(x+1)x-5
=x15-x15-x14+x14+x13-x13-x12+...-x3-x2+x2+x-5
=x-5
=>A=7-5=2
Vậy A=2 khi x=7
\(B=x^{15}-8x^{14}+8x^{13}-8x^{12}+...+8x-5\)
\(=x^{15}-\left(x+1\right)x^{14}+\left(x+1\right)x^{13}-\left(x+1\right)x^{12}+...+\left(x+1\right)x-x+2\)
\(=x^{15}-x^{15}-x^{14}+x^{14}+x^{13}-x^{13}-x^{12}+...+x^2+x-x+2\)
\(=2\)