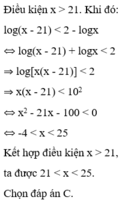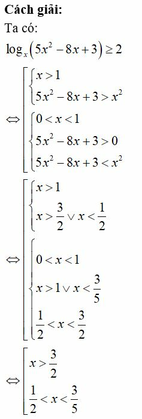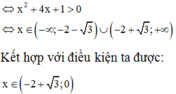Tìm S là tập hợp các nghiệm của phương trình log|x|=|logx|

Những câu hỏi liên quan
Tìm tập nghiệm của bất phương trình log ( x - 21 ) < 2 - log x
A. (-4; 25)
B. (0; 25)
C. (21; 25)
D. (25; +∞)
Tìm tất cả các nghiệm của phương trình log x + log ( x - 9 ) = 1
A. {10}
B. {9}
C. {1;9}
D. {-1;10}
Tìm tập nghiệm S của phương trình
log
x
log
x
.
A.
S
1
;
+
∞
B.
S
0
;
+
∞
C.
S
1...
Đọc tiếp
Tìm tập nghiệm S của phương trình log x = log x .
A. S = 1 ; + ∞
B. S = 0 ; + ∞
C. S = 1 ; 10
D. S = 1 ; + ∞
Đáp án D
Ta có log x = log x ⇔ x > 0 log x = log x ⇔ log x ≥ 0 log x = log x log x = − log x ⇔ x ≥ 1 log x = 0 ⇔ x ≥ 1 x = 10
Đúng 0
Bình luận (0)
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình
log
x
(
5
x
2
-
8
x
+
3
)
2
đều là nghiệm của bất phương trình
x
2
-
2
x
-
a
4
+
1
≥
0
.
Khi đó:...
Đọc tiếp
S là tập hợp tất cả các giá trị thực của tham số a thỏa mãn mỗi nghiệm của bất phương trình log x ( 5 x 2 - 8 x + 3 ) > 2 đều là nghiệm của bất phương trình x 2 - 2 x - a 4 + 1 ≥ 0 . Khi đó:
A. S = - 10 5 ; 10 5 .
B. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞
C. S = - 10 5 ; 10 5 .
D. S = - ∞ ; - 10 5 ∪ 10 5 ; + ∞ .
Tìm tập nghiệm S của bất phương trình
log
x
+
1
(
-
2
x
)
2
Đọc tiếp
Tìm tập nghiệm S của bất phương trình log x + 1 ( - 2 x ) > 2
![]()
![]()
![]()
![]()
Tìm tập nghiệm S của bất phương trình
l
o
g
x
+
1
(
-
2
x
)
2
A
.
S
(
-
1
;
0
)
B
.
S
(
-
∞
;
0
)
C
....
Đọc tiếp
Tìm tập nghiệm S của bất phương trình l o g x + 1 ( - 2 x ) > 2
A . S = ( - 1 ; 0 )
B . S = ( - ∞ ; 0 )
C . S = ( 3 - 2 ; 0 )
D . S = ( 3 - 2 ; + ∞ )
Tìm tập nghiệm của bất phương trình
log
1
2
x
+
5
2
log
x
2
A. (0; 4) B.
(
2
;
4
)
C. (-∞; 1) ∪
(
2
;
4
)
...
Đọc tiếp
Tìm tập nghiệm của bất phương trình log 1 2 x + 5 2 > log x 2
A. (0; 4)
B. ( 2 ; 4 )
C. (-∞; 1) ∪ ( 2 ; 4 )
D. (0; 1) ∪ ( 2 ; 4 )
Điều kiện: x > 0
Ta có:
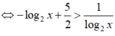
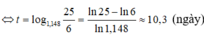
Đặt t = log 2 x , nhận được bất phương trình
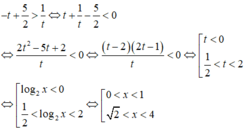
Chọn D
Đúng 0
Bình luận (0)
Giải phương trình logx = log(x + 3) - log(x - 1)
A. x = 1
B. x = 3
C. x = 4
D. x = -1, x = 3
Điều kiện x > 1. Khi đó phương trình tương đương với
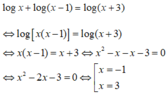
Loại nghiệm x = -1 do không thỏa mãn điều kiện. Phương trình có một nghiệm x = 3.
Chọn đáp án B.
Đúng 0
Bình luận (0)
Tập nghiệm của bất phương trình
log
2
x
-
1
≥
log
x
là
Đọc tiếp
Tập nghiệm của bất phương trình log 2 x - 1 ≥ log x là
![]()
![]()
![]()
![]()