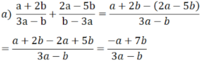Thực hiện phép tính
a) 3a(2a+b)
b) (4a5-12a3+6a2) : 2a2

Những câu hỏi liên quan
Bài 1: Thực hiện phép tính a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4); b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b); c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3); d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b) e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).Bµi 2. Viết các biểu thức sau dưới dạng đa thức a) (2a - b)(b + 4a) + 2a(b - 3a); b) (3a - 2b)(2a - 3b) - 6a(a - b); c) 5b(2x - b) - (8b - x)(2x - b); d) 2x(a + 1...
Đọc tiếp
Bài 1: Thực hiện phép tính
a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4);
b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b);
c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3);
d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b)
e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).
Bµi 2. Viết các biểu thức sau dưới dạng đa thức
a) (2a - b)(b + 4a) + 2a(b - 3a);
b) (3a - 2b)(2a - 3b) - 6a(a - b);
c) 5b(2x - b) - (8b - x)(2x - b);
d) 2x(a + 15x) + (x - 6a)(5a + 2x);
Bài 3: Chứng minh rằng các biểu thức sau không phụ thuộc vào biến
a) (y - 5)(y + 8) - (y + 4)(y - 1); b) y4 - (y2 - 1)(y2 + 1);
Bài 3:
a: Ta có: \(\left(y-5\right)\left(y+8\right)-\left(y+4\right)\left(y-1\right)\)
\(=y^2+8y-5y-40-y^2+y-4y+4\)
=-36
b: Ta có: \(y^4-\left(y^2-1\right)\left(y^2+1\right)\)
\(=y^4-y^4+1\)
=1
Đúng 0
Bình luận (0)
Bài 2:
a: \(\left(2a-b\right)\left(4a+b\right)+2a\left(b-3a\right)\)
\(=8a^2+2ab-4ab-b^2+2ab-6a^2\)
\(=2a^2-b^2\)
b: \(\left(3a-2b\right)\left(2a-3b\right)-6a\left(a-b\right)\)
\(=6a^2-9ab-4ab+6b^2-6a^2+6ab\)
\(=6b^2-7ab\)
c: \(5b\left(2x-b\right)-\left(8b-x\right)\left(2x-b\right)\)
\(=10bx-5b^2-16bx+8b^2+2x^2-xb\)
\(=3b^2-7xb+2x^2\)
Đúng 0
Bình luận (0)
Thực hiện phép tính g) (x + 2)(1 + x - x2 + x3 - x4) - (1 - x)(1 + x +x2 + x3 + x4); a) (x + 1)(1 + x - x2 + x3 - x4) - (x - 1)(1 + x + x2 + x3 + x4); b) ( 2b2 - 2 - 5b + 6b3)(3 + 3b2 - b); c) (4a - 4a4 + 2a7)(6a2 - 12 - 3a3); d) (2ab + 2a2 + b2)(2ab2 + 4a3 - 4a2b) e) (2a3 - 0,02a + 0,4a5)(0,5a6 - 0,1a2 + 0,03a4).
\(a,=x+x^2-x^3+x^4-x^5+1+x-x^2+x^3-x^4-x-x^2+x^3-x^4+x^5+1+x-x^2+x^3-x^4\\ =2x-2x^2+2x^3-2x^4\)
Đúng 3
Bình luận (0)
thực hiện phép tính
a,(3a+1)3
b,(4-2b)3
a) (3a + 1)3 = (3a)3 + 3.(3a)2.1 + 3.3a.12 + 13
= 27a3 + 27a2 + 9a + 1
b) (4 - 2b)3 = 43 - 3.42.2b + 3.4.(2b)2 - (2b)3
= 64 - 96b + 48b2 - 8b3
Đúng 2
Bình luận (0)
Thực hiện các phép tính sau:
a ) a + 2 b 3 a - b + 2 a - 5 b b - 3 a
Thực hiện các phép tính sau:a)
x
6
+
2
x
3
+
3
x
3
−
1
.
3
x
x
+
1
....
Đọc tiếp
Thực hiện các phép tính sau:
a) x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 với x ≠ ± 1 ;
b) a 3 + 2 a 2 − a − 2 3 a + 15 . 1 a − 1 − 2 a + 1 + 1 a + 2 với a ≠ − 5 ; − 2 ; ± 1 .
a) Ta có x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 = 3 x x 2 − 1
b) Gợi ý: a 3 + 2 a 2 - a - 2 = (a - 1)(a + 1) (a + 2)
Thực hiện phép tính từ trái qua phải thu được: = 1 3
Đúng 0
Bình luận (0)
thực hiện phép tính
a. A = \(\left(-\dfrac{2}{3}x^5+\dfrac{3}{4}x^4y^3-\dfrac{4}{5}x^3y^4\right):\left(-6x^2y^2\right)\)
b.B = \(\dfrac{2a-b}{a+1}-\dfrac{a^2-2a+1}{b-2}:\dfrac{a^2-1}{b^2-4}\)
\(A=\dfrac{x^3}{9y^2}-\dfrac{1}{8}x^2y+\dfrac{2}{15}xy^2\\ B=\dfrac{2a-b}{a+1}-\dfrac{\left(a-1\right)^2}{b-2}\cdot\dfrac{\left(b-2\right)\left(b+2\right)}{\left(a-1\right)\left(a+1\right)}\\ B=\dfrac{2a-b}{a+1}-\dfrac{\left(a-1\right)\left(b+2\right)}{a+1}\\ B=\dfrac{2a-b-\left(a-1\right)\left(b+2\right)}{a+1}\\ B=\dfrac{2a-b-ab-2a+b+2}{a+1}=\dfrac{2-ab}{a+1}\)
Đúng 2
Bình luận (0)
Câu 1: Thực hiện phép tính
a. ![]() b.
b. ![]()
c.![]()
Thực hiện các phép tính sau:a)
x
2
6
x
+
12
+
4
x
+
4
6
x
+
12
với
x
≠
−
2
;
b) ...
Đọc tiếp
Thực hiện các phép tính sau:
a) x 2 6 x + 12 + 4 x + 4 6 x + 12 với x ≠ − 2 ;
b) 3 a + 7 5 a 2 b + 2 a + 2 5 a 2 b với a ≠ 0 và b ≠ 0 .
a) Ta được: ( x + 2 ) 2 6 ( x + 2 ) = x + 2 6 ;
b) Ta được: 5 a + 9 5 a 2 b .
Đúng 0
Bình luận (0)
Bài 1: Thực hiện phép tínha) b) c) d) e) f)
Đọc tiếp
Bài 1: Thực hiện phép tính
a) ![]() b)
b) ![]()
c) ![]() d)
d) ![]()
e) ![]() f)
f) ![]()