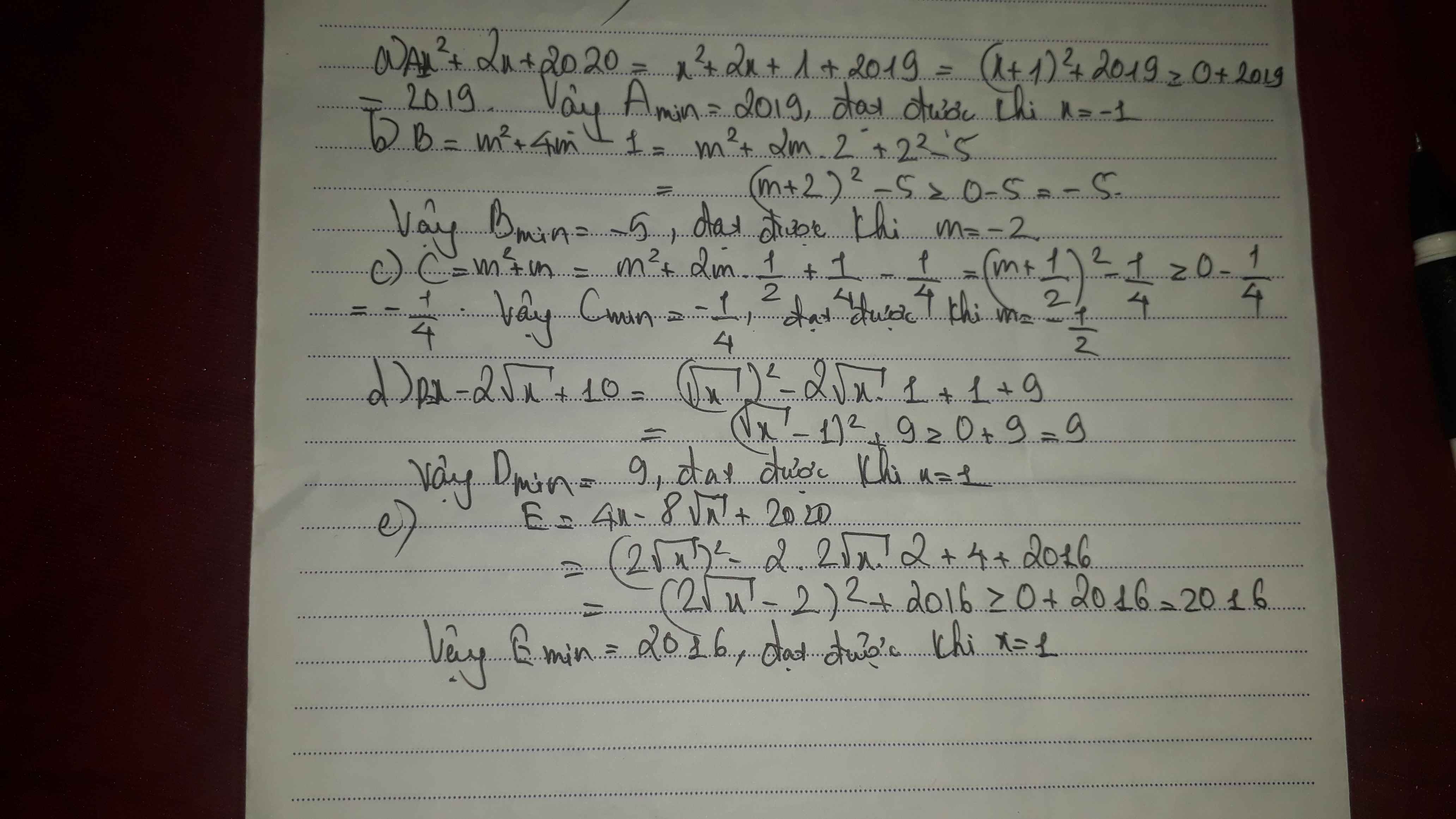\(a,=x^2+2x+1+2019=\left(x+1\right)^2+2019\ge2019\) dấu"=" xảy ra<=>x=-1

b,\(=m^2+2.2m+4-5=\left(m+2\right)^2-5\ge-5\) dấu"=" xảy ra<=>m=-2

c, \(=x-2\sqrt{x}+10=x-2\sqrt{x}+1+9=\left(\sqrt{x}-1\right)^2+9\ge9\)

dấu"=" xảy ra<=>x=1

b, \(4x-8\sqrt{x}+2020=4x-2.2.2\sqrt{x}+4+2016=\left(2\sqrt{x}-2\right)^2+2016\ge2016\)

dấu"=" xảy ra<=>x=1

a) Ta có: \(x^2+2x+2020\)

\(=x^2+2x+1+2019\)

\(=\left(x+1\right)^2+2019\ge2019\forall x\)

Dấu '=' xảy ra khi x=-1

b) Ta có: \(m^2+4m-1\)

\(=m^2+4m+4-5\)

\(=\left(m+2\right)^2-5\ge-5\forall m\)

Dấu '=' xảy ra khi m=-2

c) Ta có: \(m^2+m\)

\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}-\dfrac{1}{4}\)

\(=\left(m+\dfrac{1}{2}\right)^2-\dfrac{1}{4}\ge-\dfrac{1}{4}\forall m\)

Dấu '=' xảy ra khi \(m=-\dfrac{1}{2}\)

\(A=2\sqrt{x-1}+\sqrt{10-4x}\)

\(=\sqrt{4x-4}+\sqrt{10-4x}\)

Áp dung BĐT Bun-hia-cop-xki:

\(|\sqrt{4x-4}+\sqrt{10-4x}|\le\sqrt{1+1}.\sqrt{4x-4+10-4x}=2\sqrt{3}\)

\(\Rightarrow-2\sqrt{3}\le A\le2\sqrt{3}\)

Dấu '=' xảy ra khi \(x=\frac{7}{4}\)

Ta có 4M = 4a² + 4ab + 4b² - 12a - 12b + 8052

= (4a² + 4ab + b²) - 6(2a + b) + 9 + 3b² - 6b + 3 + 8040

= (2a + b)² - 6(a + b) + 9 + 3(b² - 2b + 1) + 8040 

= (2a + b - 3)² + 3(b - 1)² + 8040 \(\ge\)8040

=> Min 4M = 8040

=> Min M = 2010

Dấu "=" xảy ra <=> \(\hept{\begin{cases}2a+b-3=0\\b-1=0\end{cases}}\Leftrightarrow\hept{\begin{cases}a=1\\b=1\end{cases}}\Leftrightarrow a=b=1\)

Vạy Min M = 2010 <=> a = b = 1

Cách làm dài bạn thông cảm mình  nghĩ được có zậy thui ak :/

Ta có a, b là các số thực dương 

Từ \(a+3b=ab\Leftrightarrow\frac{1}{b}+\frac{3}{a}=1\ge2\sqrt{\frac{3}{ab}}.\)(bất đẳng thức Cauchy cho 2 số không âm)

\(\Leftrightarrow\frac{12}{ab}\le1\Leftrightarrow ab\ge12\)\(\Leftrightarrow84ab-72ab\ge144\Leftrightarrow84ab\ge72\left(ab+2\right)\)

\(\Leftrightarrow\frac{12ab}{ab+2}\ge\frac{72}{7}\left(1\right)\)

Ta có \(P=\frac{a^2}{1+3b}+\frac{9b^2}{1+a}\ge2\sqrt{\frac{a^2}{1+3b}\frac{9b^2}{1+a}}=\frac{6ab}{\sqrt{\left(1+a\right)\left(1+3b\right)}}\)(Bất đẳng thức Cauchy)

                                                      \(\ge\frac{6ab}{\frac{1+a+1+3b}{2}}=\frac{12ab}{a+3b+2}=\frac{12ab}{ab+2}\)(Bất đẳng thức Cauchy ngược dấu )

Kết hợp với (1) ta được :

\(P\ge\frac{12ab}{ab+2}\ge\frac{72}{7}.\)

Vậy giá trị nhỏ nhất của \(P=\frac{72}{7}\Leftrightarrow\hept{\begin{cases}a=3b\\a+3b=ab\end{cases}\Leftrightarrow\hept{\begin{cases}a=6\\b=2\end{cases}.}}\)

Ta có: \(a^2-ab+3b^2+1=\left(a^2-2ab+b^2\right)+ab+\left(b^2+1\right)+b^2\)

\(=\left(a-b\right)^2+ab+\left(b^2+1\right)+b^2\ge ab+2b+b^2\)

\(=b\left(a+b+2\right)\Rightarrow\frac{1}{\sqrt{a^2-ab+3b^2+1}}\le\frac{1}{\sqrt{b\left(a+b+2\right)}}\)(1)

Tương tự: \(\frac{1}{\sqrt{b^2-bc+3c^2+1}}\le\frac{1}{\sqrt{c\left(b+c+2\right)}}\)(2); \(\frac{1}{\sqrt{c^2-ca+3a^2+1}}\le\frac{1}{\sqrt{a\left(c+a+2\right)}}\)(3)

Cộng theo vế của 3 BĐT (1), (2), (3) và sử dụng AM - GM kết hợp liên tục BĐT \(\frac{1}{x+y}\le\frac{1}{4}\left(\frac{1}{x}+\frac{1}{y}\right)\), ta được:

\(P\le\frac{1}{\sqrt{b\left(a+b+2\right)}}+\frac{1}{\sqrt{c\left(b+c+2\right)}}+\frac{1}{\sqrt{a\left(c+a+2\right)}}\)

\(=\Sigma\frac{2}{\sqrt{4b\left(a+b+2\right)}}\)\(\le\Sigma\left(\frac{1}{4b}+\frac{1}{a+b+2}\right)\)(AM - GM)

\(=\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+\text{​​}\Sigma\left(\frac{1}{a+b+2}\right)\)

\(\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+\text{​​}\Sigma\left[\frac{1}{4}\left(\frac{1}{a+b}\right)+\frac{1}{2}\right]\)

\(\le\frac{3}{4}+\text{​​}\left[\frac{1}{8}+\frac{1}{8}+\frac{1}{8}+\text{​​}\Sigma\frac{1}{16}\left(\frac{1}{a}+\frac{1}{b}\right)\right]\)

\(=\frac{3}{4}+\text{​​}\left[\frac{3}{8}+\text{​​}\frac{1}{8}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\right]\le\frac{3}{4}+\frac{3}{8}+\frac{3}{8}=\frac{3}{2}\)

Đẳng thức xảy ra khi a = b = c = 1

Dòng thứ 10 sửa lại cho mình là \(\le\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)+\Sigma\left[\frac{1}{4}\left(\frac{1}{a+b}+\frac{1}{2}\right)\right]\)

Do olm có lỗi là mỗi lần bấm dấu ngoặc là số nó tự động nhảy ra ngoài

Cách khác

Ta đi chứng minh \(\sqrt{ab+3b^2+1}\ge\frac{a+5b+2}{4}\)

\(\Leftrightarrow16\left(ab+3b^2+1\right)\ge\left(a+5b+2\right)^2\)

\(\Leftrightarrow13\left(a-b\right)^2+10\left(b-1\right)^2+2\left(a-1\right)^2\ge0\)  ( luôn đúng )

Khi đó \(P\le\frac{4}{a+5b+2}+\frac{4}{b+5c+2}+\frac{4}{c+5a+2}\)

\(\le\frac{1}{a+b+2}+\frac{1}{4b}+\frac{1}{b+c+2}+\frac{1}{4c}+\frac{1}{c+a+2}+\frac{1}{4a}\)

\(\le\frac{1}{16}\left(\frac{2}{a}+\frac{2}{b}+\frac{2}{c}+6\right)+\frac{1}{4}\left(\frac{1}{a}+\frac{1}{b}+\frac{1}{c}\right)\)

\(\le\frac{12}{16}+\frac{3}{4}=\frac{3}{2}\)

Đẳng thức xảy ra tại a=b=c=1

\(A=2\sqrt{3}+\sqrt{\left(2+\sqrt{3}\right)^2}\\ =2\sqrt{3}+\left|2+\sqrt{3}\right|\\ =2\sqrt{3}+2+\sqrt{3}\\ =3\sqrt{3}+2\)

Với \(a;b\ge0\) đặt \(\left\{{}\begin{matrix}\sqrt{a}=x\\\sqrt{b}=y\end{matrix}\right.\) cho dễ nhìn

\(P=x^2-2xy+3y^2-2x+1\)

\(3P=3x^2-6xy+9y^2-6x+3\)

\(3P=\left(x-3y\right)^2+2\left(x-\frac{3}{2}\right)^2-\frac{3}{2}\ge-\frac{3}{2}\)

\(\Rightarrow P\ge-\frac{1}{2}\)

Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x=\frac{3}{2}\\y=\frac{1}{2}\end{matrix}\right.\) hay \(\left\{{}\begin{matrix}a=\frac{9}{4}\\x=\frac{1}{4}\end{matrix}\right.\)