Cung nhỏ AB của đường tròn (O;R) có số đo là 120o. Vậy diện tích hình quạt AOB là. A. \(\frac{\pi R^2}{6}\) B. \(\frac{\pi R^2}{4}\) C. \(\frac{\pi R^2}{3}\) D. \(\frac{\pi R^2}{2}\)

Những câu hỏi liên quan
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2 TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
Đọc tiếp
cho đường tròn tâm o đường kính AB trên cùng 1 nửa đường tròn (O) đường kính AB lấy 2 điểm C và D sao cho cung AC nhỏ ho7n cung AD .Gọi T là giao điểm của CD và AB .Vẽ đường tròn tâm I đường kính TO cắt đường tròn tâm O tại M và N (M nằ giũa cung nhỏ CD ) nối MN cắt AB tại E . cHỨNG MINH TM là tiếp tuyến của đường tròn (O) chứng minh TM^2= TC.TD . 4 điểm o, d,c,e cùng nằm trên đường tròn
a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)
b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)
\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)
c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)
mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)
mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)
Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)
\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp
Đúng 0
Bình luận (0)
Cho hai đường tròn (O) và (O') có O thuộc (O') và O' thuộc (O). Gọi A và B là các giao điểm của
hai đường tròn trên. Tính số đo cung nhỏ AB, cung lớn AB của mỗi đường tròn.
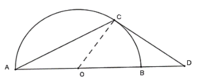
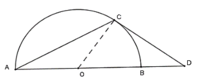
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB(cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC A.
40
°
B.
45
°
C.
60
°
D.
30
°
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB(cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC
A. 40 °
B. 45 °
C. 60 °
D. 30 °
Cho hai đường tròn đồng tâm (O;R) và (O; ). Trên đường tròn nhỏ lấy một điểm M . Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B. Tia OM cắt đường tròn lớn tại C. a) Chứng minh rằng = ( cung CA bằng cung CB) b) Tính số đo của hai cung AB
Cho AB là dây cung của đường tròn (O; 4 cm), biết AB 4 cm, số đo của cung nhỏ AB là: A.
60
0
B.
120
0
C.
30
0
D.
90
0
Đọc tiếp
Cho AB là dây cung của đường tròn (O; 4 cm), biết AB = 4 cm, số đo của cung nhỏ AB là:
A. 60 0
B. 120 0
C. 30 0
D. 90 0
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC. A.
40
°
B.
45
°
C.
60
°
D.
30
°
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung AB (cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC.
A. 40 °
B. 45 °
C. 60 °
D. 30 °
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) nhỏ hơn số đo cung nhỏ AB của (O’ ;R’)
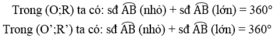
Vì số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O’;R’) nên số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O’;R’)
Như vậy, trường hợp này tương tự như giả thiết trong câu a.Chứng minh tương tự ta được R’ > R
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R .Dây AB của đường tròn đó chia đường tròn thành 2 cung ,trong đó cung lớn có số đo gấp 3 lần khung nhỏ .Tính độ dài AB theo R
cho đường tròn tâm o P là điểm nằm ngoài đường tròn,Kẻ cát tuyến PAB ( A nằm giữa P và B ) của đường tròn O .Dựng 2 tiếp tuyến PE,PF với đường tròn O( E,F là các tiếp điểm F thuộc cung nhỏ AB).Gọi D là điểm nằm giữa cung lớn AB .GỌI I là giao điểm giữa 2 đường thẳng DF và AB .CMR IB. EA=IA.EB ( ai làm đc là thần đồng ko nói nhiều)
Cho hai đường tròn (O; R) và (O': R) cắt nhau tại A, B. Hãy so sánh R và R' trong các trường hợp sau :
a) Số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O'; R')
b) Số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O'; R')
c) Số đo hai cung nhỏ bằng nhau.