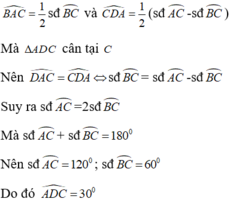Các câu hỏi tương tự
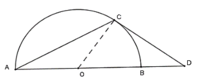
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB(cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC A.
40
°
B.
45
°
C.
60
°
D.
30
°
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB và C là điểm trên cung nhỏ AB(cung CB nhỏ hơn cung CA). Tiếp tuyến tại C của nửa đường tròn cắt đường thẳng AB tại D. Biết tam giác ADC cân tại C. Tính góc ADC
A. 40 °
B. 45 °
C. 60 °
D. 30 °
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F a) chứng minh BDCF là tứ giác nội tiếp đường trònb) chứng minh CD2 CE.CFc) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB d) K...
Đọc tiếp
Cho nửa đường tròn tâm O đường kính AB. Gọi C là một điểm trên nửa đường tròn sao cho cung CA nhỏ hơn cung CB. Trên nửa mặt phẳng bờ AB chứa điểm C, kẻ hai tia Ax và By cùng vuông góc với AB.Một đường tròn đi qua A và C (khác với đường tròn đường kính AB) cắt đường kính AB tại D và cắt Ax tại E.đường thẳng EC cắt tia By tại F
a) chứng minh BDCF là tứ giác nội tiếp đường tròn
b) chứng minh CD2 =CE.CF
c) Gọi I là giao điểm của AC và DE, J là giao điểm của BC và DF. Chứng minh IJ song song với AB
d) Khi EF là tiếp tuyến của nửa đường tròn đường kính AB thì D nằm ở vị trí nào trên AB
Cho nửa (O) đường kính AB. Kể tiếp tuyến Bx với nữa (O). C là 1 điểm trên nửa đường tròn sao cung CB= cung CA. D là điểm tùy ý trên cung CB ( D khác C, D khác B) AC cắt Bx tại E. AD cắt Bx tại F a. CM: ∆ ABE vuông cân b. FB bình = FD× FA c . CM: tứ giác CDFE nội tiếp
Cho nửa đường tròn (O) đường kính AB 2R, dây cung AC. Gọi M là điểm chính giữa cung AC. Đường thẳng kẻ từ C song song với BM cắt tia AM ở K và cắt tia OM ở D. OD cắt AC tại H.1. Chứng minh tứ giác CKMH nội tiếp.2. Chứng minh CD MB và DM CB.3. Xác định vị trí điểm C trên nửa đường tròn (O) để AD là tiếp tuyến của nửa đường tròn.4. Trong trường hợp AD là tiếp tuyến cửa nửa đường tròn (O), tính diện tích phần tam giác ADC ở ngoài đường tròn (O) theo R.
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB= 2R, dây cung AC. Gọi M là điểm chính giữa cung AC. Đường thẳng kẻ từ C song song với BM cắt tia AM ở K và cắt tia OM ở D. OD cắt AC tại H.
1. Chứng minh tứ giác CKMH nội tiếp.
2. Chứng minh CD = MB và DM = CB.
3. Xác định vị trí điểm C trên nửa đường tròn (O) để AD là tiếp tuyến của nửa đường tròn.
4. Trong trường hợp AD là tiếp tuyến cửa nửa đường tròn (O), tính diện tích phần tam giác ADC ở ngoài đường tròn (O) theo R.
Cho nửa đường tròn O đường kính AB. Kẻ tiếp tuyến Bx với nửa đường tròn . Gọi C là điểm trên nửa đường tròn sao cho cung CB = cung CA , D là 1 điểm tùy ý trên cung CB (D ≠ C, B) Các tia AC , AD cắt tia Bx theo thứ tự là E và F. Chứng minh tam giác ABC vuông cân. A
Cho nửa đường tròn (O) đường kính AB kẻ tiếp tuyến Bx với nửa đường tròn, gọi C là điểm trên nửa đường tròn sao cho cung CB bằng cung CA. D là một điểm tùy ý trên cung CD (D khác C và B) Các tia AC, AD cắt tia Bx theo thứ tự E và F a, CM tam giác ABE vuông cân b, FB^2 = FD.FA c, CM AD.AF= AC.AE Giúp em với ạ. Cảm ơn ạ^^
Cho nửa đường tròn tâm O đường kính AB , kẻ tiếp tuyến Bx với nửa đường tròn, gọi C là điểm trên nửa đường tròn sao cho cung CA bằng cung CB, D là điểm tuỳ ý trên trục khung CB , các tia AC, AD cắt tia BX theo thứ tự tại E và F a, Tính số đo góc AEB b, Chứng minh tứ giác CDFE nội tiếp đường tròn
Mình còn câu d nữa.
Cho đường tròn (O, R) đường kính AB dây cung BC=R. Đường thẳng qua O và vuông góc với AC cắt tiếp tuyến tại A của (O) ở D.
b, C/m OD là trung trực của AC. Tam giác ADC là tam giác gì
c,C/m DC là tiếp tuyến của (O)
d, Đường thẳng OD cắt đường tròn (O) tại I. C/m I là tâm đường tròn nội tiếp tam giác ADC.
Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E. . Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB tại F khác B.Chọn khẳng định sai ? A. Tứ giác BDEH nội tiếp B.
A
C
2
AE.AD C. EF // AB. D. Có 2 phương án sai .
Đọc tiếp
Cho nửa đường tròn (O) đường kính AB, trên nửa đường tròn lấy điểm C (C không trùng với A, B). Gọi H là hình chiếu của C trên đường thẳng AB. Trên cung CB lấy điểm D (D khác C, B), Hai đường thẳng AD và CH cắt nhau tại E. . Gọi (O’) là đường tròn đi qua D và tiếp xúc với AB tại B. Đường tròn (O’) cắt CB tại F khác B.
Chọn khẳng định sai ?
A. Tứ giác BDEH nội tiếp
B. A C 2 = AE.AD
C. EF // AB.
D. Có 2 phương án sai .