Cho tam giác ABC nội tiếp đường tròn (O) đường kính AC (BA<BC). Trên đoạn thẳng OC lấy điểm I bất kì (\(I\ne C\)). Đường thẳng BI cắt đường tròn (O) tại điểm thứ hai là D. Kẻ đường thẳng CH vuông góc với BD (\(H\in BD\)), DK vuông góc với AC (\(K\in AC\)). a) Chứng minh tứ giác DHKC là tứ giác nội tiếp. b) Cho độ dài đoạn thẳng AC là 4cm và góc ABD = 60o. Tính diện tích tam giác ACD. c) Đường thẳng đi qua K // BC cắt BD tại E. Chứng minh rằng khi I thay đổi trên đoạn thẳng OC (\(I\ne C\)) thì điểm E luôn thuộc một đường tròn cố định.

Những câu hỏi liên quan
Cho tam giác ABC (AB<AC) có 3 góc nhọn nội tiếp đường tròn O bán kính R. Ba đường cao AD,BE,CF cắt nhau tại H. Gọi I là tâm đường tròn nội tiếp tam giác ABC, J là tâm đường tròn bàng tiếp góc A. Chứng minh: AI.AJ=AB.AC
Cho tam giác ABC có ba góc nhọn, AB AC nội tiếp đường tròn (O). Gọi điểm I là tâm đường tròn nội tiếp tam giác ABC. Tia AI cắt đoạn BC tại điểm J, cắt đường tròn (O) tại điểm thứ hai M (M khác A)1) Chứng minh MI2 MJ. MA2, Kẻ đường kính MN của đường tròn (O). Đường thẳng AN cắt các tia phân giác trong của góc ABC và góc ACB lần lượt tại các điểm P và Q. Chứng minh N là tung điểm của đoạn thẳng PQ3, lấy điểm E bất kỳ thuộc cung nhỏ MC của đường tròn (O) (E khác M). Gọi F là điểm đối xứng với điể...
Đọc tiếp
Cho tam giác ABC có ba góc nhọn, AB < AC nội tiếp đường tròn (O). Gọi điểm I là tâm đường tròn nội tiếp tam giác ABC. Tia AI cắt đoạn BC tại điểm J, cắt đường tròn (O) tại điểm thứ hai M (M khác A)
1) Chứng minh MI2 = MJ. MA
2, Kẻ đường kính MN của đường tròn (O). Đường thẳng AN cắt các tia phân giác trong của góc ABC và góc ACB lần lượt tại các điểm P và Q. Chứng minh N là tung điểm của đoạn thẳng PQ
3, lấy điểm E bất kỳ thuộc cung nhỏ MC của đường tròn (O) (E khác M). Gọi F là điểm đối xứng với điểm I qua điểm E. Gọi R là giao điểm của hai đường thẳng PC và QB. Chứng minh 4 điểm P, Q, R, F cùng thuộc một đường tròn
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp đường tròn ( O, R) , AD là đường cao của tam giác ABC và AM là đường kính của đường tròn (O), gọi E là hình chiếu của B trên AM. a) CMR : góc ACM = 90° và BAC=MAC b) CMR : Tứ giác ABDE nội tiếp c) CM : DE // MC
a: góc ACM=1/2*sđ cung AM=90 độ
b: góc ADB=góc AEB=90 độ
=>ABDE nội tiếp
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB < AC) có ba góc nhọn nội tiếp trong đường tròn tâm O, bán kính R. Gọi H là giao điểm của ba đường cao AD, BE, CF của tam giác ABC.
1. Chứng minh rằng AEHF và AEDB là các tứ giác nội tiếp đường tròn.
2. Vẽ đường kính AK của đường tròn (O). Chứng minh tam giác ABD và tam giác AKC đồng dạng với nhau.
3. Chứng minh rằng OC vuông góc với DE.
ta có
\(\widehat{AEH}=90^0;\widehat{AFH}=90^0\)
=> \(\widehat{AEH}+\widehat{AFH}=180^0\)
=> tứ giác AEHF nội tiếp được nhé
ta lại có AEB=ADB=90 độ
=> E , D cùng nhìn cạnh AB dưới 1 góc zuông
=> tứ giác AEDB nội tiếp được nha
b)ta có góc ACK = 90 độ ( góc nội tiếp chắn nửa đường tròn)
hai tam giác zuông ADB zà ACK có
ABD = AKC ( góc nội tiếp chắn cung AC )
=> tam giác ABD ~ tam giác AKC (g.g)
c) zẽ tiếp tuyến xy tại C của (O)
ta có OC \(\perp\) Cx (1)
=> góc ABC = góc DEC
mà góc ABC = góc ACx
nên góc ACx= góc DEC
do đó Cx//DE ( 2)
từ 1 zà 2 suy ra \(OC\perp DE\)
cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn (o). các đường cao AD,BE của tam giác ABC cắt nhau tại H
a) c/m tứ giác ABDE nội tiếp
b) trong đường tròn (o) vẽ đường kính AK gọi N là giao điểm của AD vad BK chứng minh EM/DN = EH/DH
c) DE cắt MN tại I chứng minh IM=IN
a: góc AEB=góc ADB=90 độ
=>AEDB nội tiếp
b,c: M ở đâu vậy bạn?
Đúng 0
Bình luận (0)
Cho tam giác ABC (AB<AC) có ba góc nhọn nội tiếp đường tròn tâm (O) bán kính R gọi H là giao của ba đường cao AD, BE, CF của tam giác ABC .Gọi S la diện tích tam giác ABC
cho tam giác ABC ( AB < AC) có ba góc nhọn nội tiếp đường tròn (O). Các đường cao BD, CE của tam giác ABC cắt nhau tại H.
1. Cm tg AEDH, BCDE nội tiếp
2. Cm OA vuông góc với DE
3. Đường tròn đường kính AH cắt đt (O) tại F ( F khác A). cm các đường thẳng DE, BC, AF đồng duy
Em chỉ cần câu 3 thôi ạ, em cảm ơn
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn ( O ). Ba đường cao AD,BE,CF cắt nhau tại H. a) Chứng minh tứ giác AFHE là tứ giác nội tiếp. b) Vẽ đường kính AK của ( O ). Chứng minh : AB×AC = AD×AK
Lời giải:
a) Tứ giác $AFHE$ có tổng 2 góc đối nhau $\widehat{AFH}+\widehat{AEH}=90^0+90^0=180^0$ nên $AFHE$ là tứ giác nội tiếp.
b) $AK$ là đường kính thì $\widehat{ACK}=90^0$ (góc nt chắn nửa đường tròn)
Xét tam giác $ABD$ và $AKC$ có:
$\widehat{ADB}=\widehat{ACK}=90^0$
$\widehat{ABD}=\widehat{AKC}$ (góc nt cùng chắn cung $AC$)
$\Rightarrow \triangle ABD\sim \triangle AKC$ (g.g)
$\Rightarrow \frac{AB}{AD}=\frac{AK}{AC}$
$\Rightarrow AB.AC=AD.AK$ (đpcm)
Đúng 2
Bình luận (0)
cho tam giác ABC nhọn có ABAC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC2R.AD2. chứng minh HK đi qua tring điểm M của BC3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2R^2-r^24. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Đọc tiếp
cho tam giác ABC nhọn có AB<AC nội tiếp đường tròn tâm O , bán kính R . gọi H là giao điểm của 3 đường cao AD,BE,CF của tam giác ABC . kẻ đường kính AK của đường tròn (O) , AD cắt (O) tại điểm N
1. chứng minh AEDB , AEHF là tứ giác nội tiếp và AB.AC=2R.AD
2. chứng minh HK đi qua tring điểm M của BC
3. gọi bán kính đường tròn ngoại tiếp tứ giác AEHF là r . chứng minh OM^2=R^2-r^2
4. chứng minh OC vuông góc với DE và N đối xứng với H qua đường thẳng BC
Cho tam giác ABC vuông tại A. Đường tròn (O) nội tiếp tam giác ABC tiếp xúc với AB, AC lần lượt tại D và E. Tính bán kính của đường tròn (O) biết AB = 3cm, AC = 4cm.
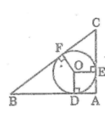
Áp dụng định lí Pitago vào tam giác vuông ABC ta có :
B C 2 = A B 2 + A C 2 = 3 2 + 4 2 = 25
Suy ra : BC = 5 (cm)
Theo tính chất hai tiếp tuyến giao nhau ta có:
AD = AE
BD = BF
CE = CF
Mà: AD = AB – BD
AE = AC – CF
Suy ra: AD + AE = AB – BD + (AC – CF)
= AB + AC – (BD + CF)
= AB + AC – (BF + CF)
= AB + AC – BC
Suy ra:
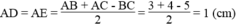
Đúng 0
Bình luận (0)

















