Kẻ AH vuông góc với BC,suy ra AH=32 cm và A,O,H thảng hàng.

Mà AH>CH >>>O nằm giữa A và H.Kẻ OM vuông góc với AC suy ra tam giác AMO đồng dạng với AHC>>>AM/AH=AO/AC

>>>20/32=(32-OH)/40>>>OH=7cm >>>khoảng cách là 7 cm

Kẻ Đường kính AD sao cho A , O , D , H thẳng hàng . 

HB = HC = BC : 2 = 24 

Tam giác AHC vuông tại H , Theo py ta go tính AH 

Tam giác ABD nội tiếp đường tròn tâm O  đường kính AD 

=> Tam giác ABD vuông tại B theo HTL tính AD 

OA = AD : 2 = .... 

OH = AH - OA 

X=7cm

Kẻ đường cao AH, ta tính được AH = 32cm.

Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM $\perp$ AC.

Ta có: $\Delta AMO\backsim \Delta AHC$ (g.g)

$\Rightarrow \frac{AO}{AC}=\frac{AM}{AH}\Rightarrow \frac{32-x}{40}=\frac{20}{32}$.

Từ đó tính được x = 7cm.

Kẻ đường cao AH, ta tính được AH = 32cm.

Do AH > HC nên tâm O nằm giữa A và H. Đặt OH = x. Kẻ OM $\perp$ AC.

Ta có: $\Delta AMO\backsim \Delta AHC$ (g.g)

\Rightarrow\frac{AO}{AC}=\frac{AM}{AH}\Rightarrow\frac{32-x}{40}=\frac{20}{32}⇒ACAO​=AHAM​⇒4032−x​=3220​.

Từ đó tính được x = 7cm.

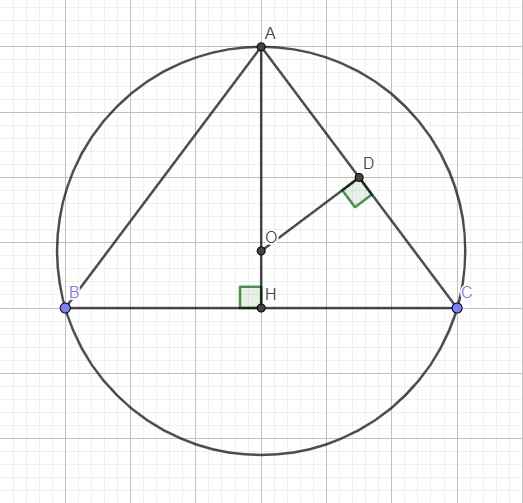
Gọi H là trung điểm BC \(\Rightarrow AH\perp BC\) và O thuộc AH do tam giác ABC cân tại A

\(CH=\dfrac{1}{2}BC=24\left(cm\right)\)

Áp dụng Pitago: \(AH=\sqrt{AC^2-CH^2}=32\left(cm\right)\)

Gọi D là trung điểm AC \(\Rightarrow\) OD là trung trực AC hay \(OD\perp AC\)

\(AD=\dfrac{1}{2}AC=20\left(cm\right)\)

Hai tam giác vuông ADO và AHC đồng dạng (chung góc A)

\(\Rightarrow\dfrac{AD}{AH}=\dfrac{AO}{AC}\Rightarrow AO=\dfrac{AD.AC}{AH}=25\left(cm\right)\)

\(\Rightarrow OH=AH-AO=7\left(cm\right)\)