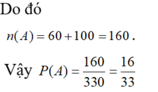trong một hộp có 14 tấm thẻ, trong đó có 5 tấm thẻ ghi số 1,4 thẻ ghi số 2,3 thẻ ghi số 3 và 2 thẻ ghi số 4. Chọn ngẫu nhiên 2 tấm thẻ từ 15 tấm thẻ trong hộp. Tính xác suất để chọn được 2 tấm thẻ có tổng các số ghi trên 2 tấm thẻ đó bằng 5

Những câu hỏi liên quan
Trong hộp có 10 tấm thẻ cùng loại, trên mỗi tấm thẻ có ghi một số tự nhiên. Lấy ra ngẫu nhiên 1 thẻ từ hộp. Biết rằng xác suất lấy được thẻ ghi số chẵn gấp 4 lần xác suất lấy được thẻ ghi số lẻ. Hỏi trong hộp có bao nhiêu thẻ ghi số lẻ?
Gọi số thẻ ghi số lẻ trong hộp là \(n\). Khi đó, xác suất tấm thẻ lấy ra ghi số lẻ là \(\frac{n}{{10}}\).
Số thẻ ghi số chẵn trong hộp là \(10 - n\). Khi đó, xác suất tấm thẻ lấy ra ghi số chẵn là \(\frac{{10 - n}}{{10}}\).
Vì xác suất lấy được thẻ chẵn gấp 4 lần xác suất lấy được thẻ lẻ nên \(\frac{{10 - n}}{{10}} = 4.\frac{n}{{10}} \Leftrightarrow 10 - n = 4n \Leftrightarrow 5n = 10 \Leftrightarrow n = 2\)
Vậy số thẻ ghi số lẻ trong hộp là 2 thẻ.
Đúng 0
Bình luận (0)
Trong 1 hộp kín có 20 tấm thẻ, ghi trên mỗi tấm thẻ là các số từ 1 đến 20 (2 tấm khác nhau thì ghi số khác nhau). Lấy ngẫu nhiên từ trong hộp đó ra 2 tấm thẻ. Tìm xác suất để tổng 2 số ghi trên 2 tấm thẻ đó chia hết cho 3. A.
p
1
2
B.
p
1
3
C.
p
32
95
D. ...
Đọc tiếp
Trong 1 hộp kín có 20 tấm thẻ, ghi trên mỗi tấm thẻ là các số từ 1 đến 20 (2 tấm khác nhau thì ghi số khác nhau). Lấy ngẫu nhiên từ trong hộp đó ra 2 tấm thẻ. Tìm xác suất để tổng 2 số ghi trên 2 tấm thẻ đó chia hết cho 3.
A. p = 1 2
B. p = 1 3
C. p = 32 95
D. p = 49 190
. Một hộp đựng 15 tấm thẻ được đánh số từ 1 đến 15 . Chọn ngẫu nhiên 5 tấm thẻ. Tính xác suất để
tổng số ghi trên 5 tấm thẻ ấy là một số lẻ.
Không gian mẫu: \(C_{15}^5\)
Tổng số 5 tấm thẻ là lẻ khi số số thẻ lẻ là 1 số lẻ, gồm các trường hợp: (1 thẻ lẻ, 4 thẻ chẵn), (3 thẻ lẻ, 2 thẻ chẵn), (5 thẻ đều lẻ)
Trong 15 tấm thẻ có 7 thẻ chẵn và 8 thẻ lẻ
\(\Rightarrow\) Số biến cố thuận lợi: \(C_8^1.C_7^4+C_8^3.C_7^2+C_8^5\)
Xác suất: ...
Đúng 2
Bình luận (0)
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng A.
16
33
B.
1
2
C.
2
11
D.
10
33
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng
A. 16 33
B. 1 2
C. 2 11
D. 10 33
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng: A.
16
33
B.
1
2
C.
2
11
D.
10
33
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
A. 16 33
B. 1 2
C. 2 11
D. 10 33
HD: Số phần tử của không gian mẫu là: Ω = C 11 4
Gọi A là biến cố: “Tổng số ghi trên 4 tấm thẻ ấy là một số lẻ”
Khi đó số tấm lẻ được chọn là số lẻ.
Trong 11 số từ 1 đến 11 có 6 số lẻ và 5 số chẵn.

Đúng 0
Bình luận (0)
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng A.
16
33
B.
1
2
C.
2
11
D.
10
33
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng
A. 16 33
B. 1 2
C. 2 11
D. 10 33
Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra
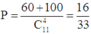
Đúng 0
Bình luận (0)
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng A.
16
33
B.
1
2
C.
2
11
D.
10
33
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng
A. 16 33
B. 1 2
C. 2 11
D. 10 33
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng A.
16
33
B.
1
2
C.
2
11
D.
10
33
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp. Gọi P là xác suất để tổng số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng
A. 16 33
B. 1 2
C. 2 11
D. 10 33
Đáp án A
Tổng cả 4 tấm thẻ là 1 số lẻ khi
+) Có 1 thẻ là lẻ, 3 thẻ còn lại là chẵn, suy ra có C 6 1 C 5 3 = 60 cách chọn.
+) Có 3 thẻ là lẻ, 1 thẻ là chẵn, suy ra có C 5 1 C 6 3 = 100 cách chọn.
Suy ra P = 60 + 100 C 11 4 = 16 33
Đúng 0
Bình luận (0)
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P là xác suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng: A.
1
12
B.
16
33
C.
10
33
D.
2
11
Đọc tiếp
Một hộp đựng 11 tấm thẻ được đánh số từ 1 đến 11. Chọn ngẫu nhiên 4 tấm thẻ từ hộp đó. Gọi P là xác suất để tổng các số ghi trên 4 tấm thẻ ấy là một số lẻ. Khi đó P bằng:
A. 1 12
B. 16 33
C. 10 33
D. 2 11