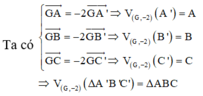Cho tam giác ABC vuông tại A AB = 6 AC = 8 phép vị tự tâm A tỷ số 3/2 đến B thành B' biến C thành C' tính bán kính R của đường tròn ngoại tiếp tam giám AB'C'

Những câu hỏi liên quan
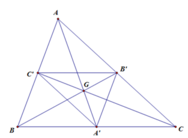
Cho tam giác ABC với trọng tâm G. Gọi A,B,C lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác ABC thành tam giác ABC là A. Phép vị tự tâm G, tỉ số k2 B. Phép vị tự tâm G, tỉ số k-2 C. Phép vị tự tâm G, tỉ số k-3 D. Phép vị tự tâm G, tỉ số k3
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác A'B'C' thành tam giác ABC là
A. Phép vị tự tâm G, tỉ số k=2
B. Phép vị tự tâm G, tỉ số k=-2
C. Phép vị tự tâm G, tỉ số k=-3
D. Phép vị tự tâm G, tỉ số k=3
Đáp án B
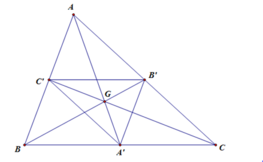
G A → = − 2 G A ' → ⇒ V G , − 2 A ' = A G B → = − 2 G B ' → ⇒ V G , − 2 B ' = B G C → = − 2 G C ' → ⇒ V G , − 2 C ' = C ⇒ V G , − 2 Δ A ' B ' C ' = Δ A B C
Đúng 0
Bình luận (0)
Cho tam giác ABC với trọng tâm G. Gọi A,B,C lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác ABC thành tam giác ABC là A. Phép vị tự tâm G, tỉ số k2 B. Phép vị tự tâm G, tỉ số k-2 C. Phép vị tự tâm G, tỉ số k-3 D. Phép vị tự tâm G, tỉ số k3
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A',B',C' lần lượt là trung điểm của các cạnh BC,AC,AB của tam giác ABC. Phép vị tự biến tam giác A'B'C' thành tam giác ABC là
A. Phép vị tự tâm G, tỉ số k=2
B. Phép vị tự tâm G, tỉ số k=-2
C. Phép vị tự tâm G, tỉ số k=-3
D. Phép vị tự tâm G, tỉ số k=3
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A’B’C thành tam giác ABC? A. Phép vị tự tâm G, tỉ số -1/2 B. Phép vị tự tâm G, tỉ số 1/2 C. Phép vị tự tâm G, tỉ số 2 D. Phép vị tự tâm G, tỉ số -2
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, AC, AB của tam giác ABC. Khi đó phép vị tự nào biến tam giác A’B’C thành tam giác ABC?
A. Phép vị tự tâm G, tỉ số -1/2
B. Phép vị tự tâm G, tỉ số 1/2
C. Phép vị tự tâm G, tỉ số 2
D. Phép vị tự tâm G, tỉ số -2
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC? A. Phép vị tự tâm G, tỉ số 2 B. Phép vị tự tâm G, tỉ số –2 C. Phép vị tự tâm G, tỉ số
−
2
3
D. Phép vị tự tâm G, tỉ số
−
1
2
Đọc tiếp
Cho tam giác ABC với trọng tâm G. Gọi A’, B’, C’ lần lượt là trung điểm các cạnh BC, AC, AB của tam giác ABC. Khi đó, phép vị tự nào biến tam giác A’B’C’ thành tam giác ABC?
A. Phép vị tự tâm G, tỉ số 2
B. Phép vị tự tâm G, tỉ số –2
C. Phép vị tự tâm G, tỉ số − 2 3
D. Phép vị tự tâm G, tỉ số − 1 2
Đáp án B
A’ = V G ; k ( A ) => − 2 G A ' → = G A → =>Tỉ số vị tự k = – 2
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến M thành B, N thành C. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Đáp án A
B = V A ; k ( M ) và 2 M A → = A B →
C = V A ; k ( N ) và 2 N A → = A C →
=>k = 2
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi M , N lần lượt là trung điểm của AB và AC. Phép vị tự tâm A tỉ số k biến B thành M, C thành N. Khi đó k bằng
A. 2
B.-2
C. 1 2
D. − 1 2
Đáp án C
M = V A ; k ( B ) và 2 M A → = A B → => k = 1 2
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A,tại đường cái AH.Biết AB=6,BC=10 1.Giải tâm giác vuống ABC(góc làm tròn đến độ,độ dài lm tròn đến hàng đơn vị. 2.Từ H kể HE vuông góc với AB (E€BA).HF vuông góc với AC(F€AC) . Chứng minh AE.AB=AF.AC
2: Xét ΔAHB vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A, AB=6, AC=8.
a) Xác định tâm đường tròn ngoại tiếp tam giác ABC
b) Tính bán kính đường tròn đó
trong mặt phảng toạn độ Oxy, cho tam giác ABC có phương trình các cạnh AB, AC lần lượt là x=0; x-y=0. phép vị tự tâm 0 tỉ số k= -3 biến tam giác A'B'C'. khi đó góc A' của tam giác A'B'C' có số đo là?