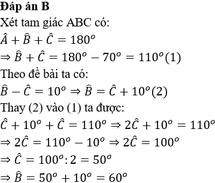Cho tam giác ABC có góc B=70o;gócC=30o.Tia phân giác của góc A cắt BC tại D.KẺ AH vuông góc BC(H thuộc BC).Tính góc BAC? góc HAD? góc ADH ?

Những câu hỏi liên quan
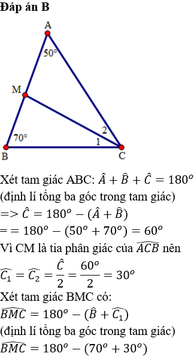
Cho tam giác ABC và tam giác DEF có góc A = 50o , góc E=70o,góc F= 60ocạnh AB=DE , AC=DF. CM tam giác ABC= tam giác DEF
\(\Delta DEF\) cho ta \(\widehat{D}+\widehat{E}+\widehat{F}=180^0\)
\(\Rightarrow\widehat{D}=180^0-\left(\widehat{E}+\widehat{F}\right)\)
\(\Rightarrow\widehat{D}=180^0-\left(70^0+60^0\right)=180^0-130^0=50^0\)
\(Xét\) \(\Delta ABCvà\Delta DEFcó\)
\(\widehat{A}=\widehat{D}\left(=50^0\right)\)
AB=DE
AC=DF
\(\Rightarrow\Delta ABC=\Delta DEF\left(c-g-c\right)\)
Vậy \(\Delta ABC=\Delta DEF\)
Đúng 1
Bình luận (0)
cho tam giác ABC có Â=50o,C=70o,góc ngoài của tam giác tại đỉnh B là:
A. 140o
B. 1000
C. 60o
D. 120o
Xem thêm câu trả lời
Cho tam giác ABC có
A
^
50
o
,
B
^
70
o
. Tia phân giác của góc C cắt AB tại M. Tính số đo góc BMC A. 60
°
B. 80
°
C. 90
°
D. 100
°
Đọc tiếp
Cho tam giác ABC có A ^ = 50 o , B ^ = 70 o . Tia phân giác của góc C cắt AB tại M. Tính số đo góc BMC
A. 60 °
B. 80 °
C. 90 °
D. 100 °
Cho tam giác ABC cân tại A, có ∠ A = 70 o . Khi đó số đo góc B là:
A. 50 o
B. 60 o
C. 55 o
D. 75 o
Số đo góc B là (180o - 70o)/2 = 55o. Chọn A
Đúng 0
Bình luận (0)
Cho tam giác ABC có
B
^
70
o
,
C
^
30
o
. Tia phân giác của góc A cắt cạnh BC tại D. Tính
A
D
C
^
A. 100
°
B. 120
°
C. 130
°
D. 110
°
Đọc tiếp
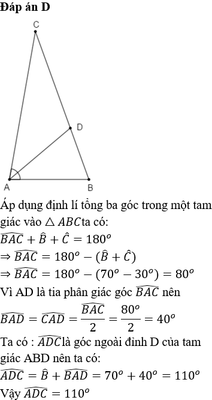
Cho tam giác ABC có B ^ = 70 o , C ^ = 30 o . Tia phân giác của góc A cắt cạnh BC tại D. Tính A D C ^
A. 100 °
B. 120 °
C. 130 °
D. 110 °
Cho tam giác ABC có
A
^
50
o
,
B
^
70
o
. Tia phân giác của góc C cắt cạnh AB tại M. Tính
A
M
C
^
,
B
M
C
^
A. ...
Đọc tiếp
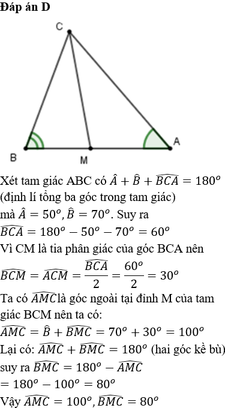
Cho tam giác ABC có A ^ = 50 o , B ^ = 70 o . Tia phân giác của góc C cắt cạnh AB tại M. Tính A M C ^ , B M C ^
A. A M C ^ = 120 ° , B M C ^ = 60 °
B. A M C ^ = 80 ° , B M C ^ = 100 °
C. A M C ^ = 110 ° , B M C ^ = 70 °
D. A M C ^ = 100 ° , B M C ^ = 80 °
Tam giác ABC có
A
^
70
o
,
B
^
-
C
^
10
o
. Số đo góc B và góc C lần lượt là: A.
B
^
70
°
,
C
^
40
°
B.
B
^
60...
Đọc tiếp
Tam giác ABC có A ^ = 70 o , B ^ - C ^ = 10 o . Số đo góc B và góc C lần lượt là:
A. B ^ = 70 ° , C ^ = 40 °
B. B ^ = 60 ° , C ^ = 50 °
C. B ^ = 70 ° , C ^ = 60 °
D. B ^ = 50 ° , C ^ = 60 °
Cho tam giác ABC có
∠
A
70
o
,
∠
B
30
o
.
I là giao diểm của ba đường phân giác. Khi đó số đo góc ∠(ACI) là: A.
70
o
B.
60
o
C.
40
o
D.
50...
Đọc tiếp
Cho tam giác ABC có ∠ A = 70 o , ∠ B = 30 o . I là giao diểm của ba đường phân giác. Khi đó số đo góc ∠(ACI) là:
A. 70 o
B. 60 o
C. 40 o
D. 50 o
Ta có ∠(ACB) = 180o - 70o - 30o = 80o
CI là tia phân giác của góc C nên ∠(ACI) = 80o : 2 = 40o. Chọn C
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(ADH)
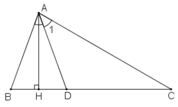
Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o
Đúng 0
Bình luận (0)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(HAD)
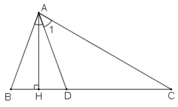
ΔADH vuông tại H nên:
∠(HAD) + ∠(ADH) = 90o (tính chất tam giác vuông)
⇒∠ (HAD) = 90o-∠(ADH)o = 90o - 70o = 20o
Đúng 0
Bình luận (0)