Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o

Ta có: ∠(A1 ) =(1/2 )∠(BAC) = (1/2).80o = 40o
(vì AD tia phân giác của góc BAC)
Trong ΔADC ta có ∠(ADH) là góc ngoài tại đỉnh D
Do đó: ∠(ADH) = ∠(A1) + ∠C (tính chất góc ngoài của tam giác)
Vậy ∠(ADH ) = 40o + 30o = 70o
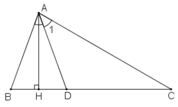
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(HAD)
Cho tam giác ABC có ∠B =70o; ∠C =30o. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc vói BC (H thuộc BC) Tính ∠(BAC)
Cho tam giác ABC vuông tại A có C ^ = 35 ° . Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC).
a) Tính góc ADH.
b) Tính góc HAD và HAB.
Cho tam giác ABC vuông tại A có C ^ = 35 ° . Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H thuộc BC).
a) Tính góc ADH.
b) Tính góc HAD và HAB.
Cho tam giác ABC có B = 70°;C= 30°. Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC ( H∈BC ) .
a ) Tính số đo BAC
b ) Tính số đo ADH
cho tam giác abc có góc b = 70 độ,góc c =30 độ tia phân giác của góc a cắt bc tại d.kẻ ah vuông góc với bc(h thuộc bc) a)tính các góc :bac,had,adh b)từ d kẻ de//ab(e thuộc ac.tính số đo các góc của ∆ ade
Cho tam giác ABC có góc B= \(70^0\), góc C=\(40^0\). Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc với BC (H ϵ BC). Tính góc BAC, góc ADH, góc HAD
Bài 2) cho tam giác ABC có góc B= 70 độ : góc C= 30 độ Tia phân giác của góc A cắt BC tại D Kẻ AH vuông góc với BC (H e BC). Tính góc BAC: góc ADH: góc HAD
Cho tam giác ABC có góc B = 60 độ ; góc C = 30 độ . Tia phân giác của góc A cắt BC tại D. Kẻ AH vuông góc BC (H thuộc BC )
a. Tính số đo các góc BAC;ADH;HAD
b. Kẻ DE // AB (E thuộc AC ); EK là phân giác góc AED. Chứng minh : EK vuông góc AD