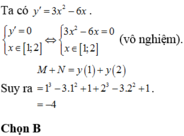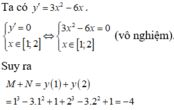Tìm GTLN của hàm số 3x2(1-x)

Những câu hỏi liên quan
Tìm số f(x) x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi. A. 0 x 2. B. x 1. C. x 0 hoặc x 1 D. x 0 hoặc x 2.
Đọc tiếp
Tìm số f(x) = x3 – 3x2 + 1. Đạo hàm của hàm số f(x) âm khi và chỉ khi.
A. 0 < x < 2.
B. x < 1.
C. x < 0 hoặc x > 1
D. x < 0 hoặc x > 2.
Chọn A.
Ta có: f’(x) = 3x2 – 6x.
f’(x) < 0 ⇔ 3x2 – 6x < 0 ⇔ 0 < x < 2.
Đúng 0
Bình luận (0)
Gọi M, N lần lượt là GTLN, TNNN của hàm số
y
x
3
-
3
x
2
+
1
trên [1;2]. Khi đó tổng M+N bằng
Đọc tiếp
Gọi M, N lần lượt là GTLN, TNNN của hàm số y = x 3 - 3 x 2 + 1 trên [1;2]. Khi đó tổng M+N bằng
![]()
![]()
![]()
![]()
Gọi M, N lần lượt là GTLN, TNNN của hàm số
y
x
3
-
3
x
2
+
1
trên [1;2]. Khi đó tổng M+N bằng A.
-
2
B.
-
4
C. 0 D. 2
Đọc tiếp
Gọi M, N lần lượt là GTLN, TNNN của hàm số y = x 3 - 3 x 2 + 1 trên [1;2]. Khi đó tổng M+N bằng
A. - 2
B. - 4
C. 0
D. 2
24. Tìm GTLN của hàm số: \(y=3\cos\left(x-\dfrac{\pi}{2}\right)+1\)
26. a) Tìm GTLN của hàm số: \(y=\cos2x+\sin2x\)
b) Giải PT: \(\sin x+\sqrt{3}\cos x=1\)
24.
\(cos\left(x-\dfrac{\pi}{2}\right)\le1\Rightarrow y\le3.1+1=4\)
\(y_{max}=4\)
26.
\(y=\sqrt{2}cos\left(2x-\dfrac{\pi}{4}\right)\)
Do \(cos\left(2x-\dfrac{\pi}{4}\right)\le1\Rightarrow y\le\sqrt{2}\)
\(y_{max}=\sqrt{2}\)
b.
\(\dfrac{1}{2}sinx+\dfrac{\sqrt{3}}{2}cosx=\dfrac{1}{2}\)
\(\Leftrightarrow cos\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{3}+k2\pi\\x-\dfrac{\pi}{6}=-\dfrac{\pi}{3}+k2\pi\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}+k2\pi\\x=-\dfrac{\pi}{6}+k2\pi\end{matrix}\right.\)
Đúng 4
Bình luận (0)
GTLN, GTNN của hàm số
y=x3 _ 3x2 - 9x + 35 trên đoạn [ -4,4] lần lược là
\(y=x^3-3x^2-9x+35\)
\(y'=3x^2-6x-9\)
\(y'=0\Leftrightarrow3x^2-6x-9=0\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(y\left(-4\right)=-41;y\left(-1\right)=40;y\left(3\right)=8;y\left(4\right)=52\)
\(\Rightarrow y_{max}=y\left(4\right)=52;y_{min}=y\left(-4\right)=-41\) trên đoạn \(\left[-4;4\right]\)
Đúng 2
Bình luận (0)
Tìm
y
C
ε
(hoặc
y
C
T
) của hàm số
y
x
+
3
x
2
+
1
Đọc tiếp
Tìm y C ε (hoặc y C T ) của hàm số y = x + 3 x 2 + 1

![]()
![]()
![]()
Tìm giá trị thực của m để hàm số
F
x
x
3
-
2
m
-
3
x
2
-
4
x
+
10
là một nguyên hàm của hàm số
f
x
3
x
2
-
12
x
-
4
với mọ...
Đọc tiếp
Tìm giá trị thực của m để hàm số F x = x 3 - 2 m - 3 x 2 - 4 x + 10 là một nguyên hàm của hàm số f x = 3 x 2 - 12 x - 4 với mọi x ∈ R
A. m = 3 2
B. m = - 9 2
C. m = 9 2
D. m = 9
Tìm nguyên hàm của hàm số
f
(
x
)
3
x
2
+
8
sin
x
.
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 3 x 2 + 8 sin x .
![]()
![]()
![]()
![]()
Tìm số đường tiệm cận của đồ thị hàm số
y
x
−
3
x
2
+
1
. A. 1 B. 2 C. 3 D. 0
Đọc tiếp
Tìm số đường tiệm cận của đồ thị hàm số y = x − 3 x 2 + 1 .
A. 1
B. 2
C. 3
D. 0
Đáp án A.
Hàm số không có tiệm cận đứng.
Có lim x → ± ∞ y = 0 ⇒ y = 0 là tiệm cận ngang.
Đúng 0
Bình luận (0)
Tìm nguyên hàm của hàm số
f
(
x
)
3
x
2
+
8
s
i
n
x
.
A.
∫
f
(
x
)
d
x
6
x
-
8
cos
x
+
C
B.
∫
f
(
x
)
d
x
6
x
+...
Đọc tiếp
Tìm nguyên hàm của hàm số f ( x ) = 3 x 2 + 8 s i n x .
A. ∫ f ( x ) d x = 6 x - 8 cos x + C
B. ∫ f ( x ) d x = 6 x + 8 cos x + C
C. ∫ f ( x ) d x = x 3 - 8 cos x + C
D. ∫ f ( x ) d x = x 3 + 8 cos x + C