giải phương trình
3x4+6x3-33x2-24x+48=0
Giải bất phương trình sau 1 x 2 - 4 < 3 3 x 2 + x - 4
Điều kiện xác định
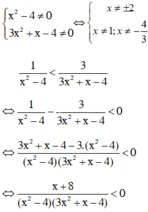
+ Nhị thức x + 8 có nghiệm x = -8
+ Tam thức x2 – 4 có hai nghiệm x = 2 và x = -2, hệ số a = 1 > 0
Do đó x2 – 4 mang dấu + khi x < -2 hoặc x > 2 và mang dấu – khi -2 < x < 2.
+ Tam thức 3x2 + x – 4 có hai nghiệm x = 1 và x = -4/3, hệ số a = 3 > 0.
Do đó 3x2 + x – 4 mang dấu + khi x < -4/3 hoặc x > 1
mang dấu – khi -4/3 < x < 1.
Ta có bảng biến thiên
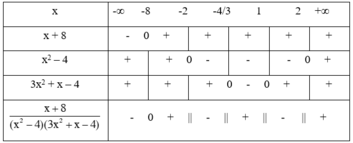
Dựa vào BBT ta thấy
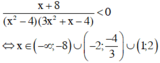
Vậy tập nghiệm của bất phương trình là: T = (-∞; -8) ∪ (-2; -4/3) ∪ (1; 2)
Giải các phương trình trùng phương:
3x4 + 10x2 + 3 = 0
3x4 + 10x2 + 3 = 0 (1)
Đặt x2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : 3t2 + 10t + 3 = 0 (2)
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ’ = 52 – 3.3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
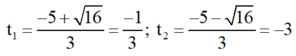
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Giải các phương trình trùng phương: 3x4 + 4x2 + 1 = 0
3x4 + 4x2 + 1 = 0
Đặt x2 = t (t ≥ 0). Phương trình trở thành:
3t2 + 4t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t1 = -1; t2 = (-1)/3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
Giải phương trình x4 – 8x3 + 21x2 -24x + 9 = 0
Ta có: \(x^4-8x^3+21x^2-24x+9=0\)
\(\Leftrightarrow x^4-5x^3+3x^2-3x^3+15x^2-9x+3x^2-5x+9=0\)
\(\Leftrightarrow\left(x^2-5x+3\right)\left(x^2-3x+3\right)=0\)
\(\Leftrightarrow x^2-5x+3=0\)
\(\text{Δ}=\left(-5\right)^2-4\cdot1\cdot3=25-12=13\)
Vì Δ>0 nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{5-\sqrt{13}}{2}\\x_2=\dfrac{5+\sqrt{13}}{2}\end{matrix}\right.\)
Giải các phương trình 3x4 + 2x2 - 1 = 0
3x4 + 2x2 – 1 = 0 (2)
Tập xác định : D = R.
Đặt t = x2, điều kiện t ≥ 0
Khi đó phương trình (2) trở thành :
3t2 + 2t – 1 = 0 ⇔ (3t – 1)(t + 1) = 0
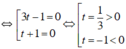
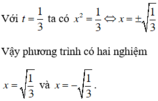
Giải các phương trình: 3x4 – 12x2 + 9 = 0
Cả ba phương trình trên đều là phương trình trùng phương.
3x4 – 12x2 + 9 = 0 (1)
Đặt x2 = t, t ≥ 0.
(1) trở thành: 3t2 – 12t + 9 = 0 (2)
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t1 = 1 và t2 = 3.
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x2 = 3 ⇒ x = ±√3.
+ t = 1 ⇒ x2 = 1 ⇒ x = ±1.
Vậy phương trình có tập nghiệm 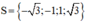
Giải các phương trình trùng phương:
a ) 4 x 4 + x 2 − 5 = 0 b ) 3 x 4 + 4 x 2 + 1 = 0
a) 4 x 4 + x 2 − 5 = 0
Đặt x 2 = t (t ≥ 0). Phương trình trở thành:
4 t 2 + t − 5 = 0
Nhận thấy phương trình có dạng a + b + c = 0 nên phương trình có nghiệm
t 1 = 1 ; t 2 = ( − 5 ) / 4
Do t ≥ 0 nên t = 1 thỏa mãn điều kiện
Với t = 1, ta có: x 2 = 1 ⇔ x = ± 1
Vậy phương trình có 2 nghiệm x 1 = 1 ; x 2 = − 1
b) 3 x 4 + 4 x 2 + 1 = 0
Đặt x 2 = t ( t ≥ 0 ) . Phương trình trở thành:
3 t 2 + 4 t + 1 = 0
Nhận thấy phương trình có dạng a - b + c = 0 nên phương trình có nghiệm
t 1 = - 1 ; t 2 = ( - 1 ) / 3
Cả 2 nghiệm của phương trình đều không thỏa mãn điều kiện t ≥ 0
Vậy phương trình đã cho vô nghiệm.
Giải các phương trình:
a ) 3 x 4 – 12 x 2 + 9 = 0 ; b ) 2 x 4 + 3 x 2 – 2 = 0 ; c ) x 4 + 5 x 2 + 1 = 0.
Cả ba phương trình trên đều là phương trình trùng phương.
a) 3 x 4 – 12 x 2 + 9 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 3 t 2 – 12 t + 9 = 0 ( 2 )
Giải (2):
Có a = 3; b = -12; c = 9
⇒ a + b + c = 0
⇒ (2) có hai nghiệm t 1 = 1 v à t 2 = 3 .
Cả hai nghiệm đều thỏa mãn điều kiện.
+ t = 3 ⇒ x 2 = 3 ⇒ x = ± 3 + t = 1 ⇒ x 2 = 1 ⇒ x = ± 1
Vậy phương trình có tập nghiệm 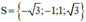
b) 2 x 4 + 3 x 2 – 2 = 0 ( 1 )
Đặt x 2 = t , t ≥ 0.
(1) trở thành: 2 t 2 + 3 t – 2 = 0 ( 2 )
Giải (2) :
Có a = 2 ; b = 3 ; c = -2
⇒ Δ = 3 2 – 4 . 2 . ( - 2 ) = 25 > 0
⇒ (2) có hai nghiệm
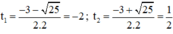
t 1 = - 2 < 0 nên loại.
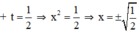
Vậy phương trình có tập nghiệm 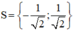
c) x 4 + 5 x 2 + 1 = 0 ( 1 )
Đặt x 2 = t , t > 0 .
(1) trở thành: t 2 + 5 t + 1 = 0 ( 2 )
Giải (2):
Có a = 1; b = 5; c = 1
⇒ Δ = 5 2 – 4 . 1 . 1 = 21 > 0
⇒ Phương trình có hai nghiệm:
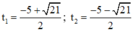
Cả hai nghiệm đều < 0 nên không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.
Giải các phương trình trùng phương:
a ) x 4 − 5 x 2 + 4 = 0 b ) 2 x 4 − 3 x 2 − 2 = 0 c ) 3 x 4 + 10 x 2 + 3 = 0
a) x 4 – 5 x 2 + 4 = 0 ( 1 )
Đặt x 2 = t, điều kiện t ≥ 0.
Khi đó (1) trở thành : t 2 – 5 t + 4 = 0 ( 2 )
Giải (2) : Có a = 1 ; b = -5 ; c = 4 ⇒ a + b + c = 0
⇒ Phương trình có hai nghiệm t 1 = 1 ; t 2 = c / a = 4
Cả hai giá trị đều thỏa mãn điều kiện.
+ Với t = 1 ⇒ x 2 = 1 ⇒ x = 1 hoặc x = -1;
+ Với t = 4 ⇒ x 2 = 4 ⇒ x = 2 hoặc x = -2.
Vậy phương trình (1) có tập nghiệm S = {-2 ; -1 ; 1 ; 2}.
b) 2 x 4 – 3 x 2 – 2 = 0 ; ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 2 t 2 – 3 t – 2 = 0 ( 2 )
Giải (2) : Có a = 2 ; b = -3 ; c = -2
⇒ Δ = ( - 3 ) 2 - 4 . 2 . ( - 2 ) = 25 > 0
⇒ Phương trình có hai nghiệm
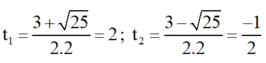
Chỉ có giá trị t 1 = 2 thỏa mãn điều kiện.
+ Với t = 2 ⇒ x 2 = 2 ⇒ x = √2 hoặc x = -√2;
Vậy phương trình (1) có tập nghiệm S = {-√2 ; √2}.
c) 3 x 4 + 10 x 2 + 3 = 0 ( 1 )
Đặt x 2 = t , điều kiện t ≥ 0.
Khi đó (1) trở thành : 3 t 2 + 10 t + 3 = 0 ( 2 )
Giải (2) : Có a = 3; b' = 5; c = 3
⇒ Δ ’ = 5 2 – 3 . 3 = 16 > 0
⇒ Phương trình có hai nghiệm phân biệt
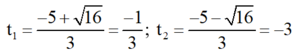
Cả hai giá trị đều không thỏa mãn điều kiện.
Vậy phương trình (1) vô nghiệm.