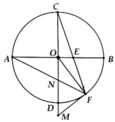
Cho đường tròn (O),đường kính AB. Trên AB lấy một điểm E, qua E vẽ dây CD vuông góc với AB. Trên đoạn thẳng BE lấy một điểm F. Vẽ các dây CM và DN đi qua F. Chứng minh CDMN là hình thang cân

Những câu hỏi liên quan
Cho đường tròn tâm o đường kính AB,E thuộc AB.Qua E vẽ dây CD vuông góc với AB.Trên đoạn BE lấy diểm F vẽ dây CM và DN đi qua F.Chứng minh rằng tứ giác CDMN là hinh thang cân
em ko bt em mới học lớp 8 à tk cho em ik
Đúng 0
Bình luận (0)
tứ giác CNMD nội tiếp đg tròn tâm 0.suy ra gốc MDF= MCN.
tam giác CNF và MFD có:
góc CFN=DFM
CF=FD
gốc MDF= MCN
=> NFC=MFD(g c g)
=> CN=FN, FN=FM (1)
gọi I là giao điểm của NM và AB
tam giác NFI=MFI=>AB vuông góc với NM mà AB vg vs CD
=> CDNM là hình thang (2)
Từ (1)(2)=> đpcm
~HỌC TỐ ~
Đúng 0
Bình luận (0)
Cho (O) đường kính AB. Trên AB lấy một điểm E. Qua E vẽ dây CD vuông góc với AB. Vẽ các dây DN; CM đi qua F. Chứng minh rằng NI = IM
I ở đâu bà nội ??? Hỏi thế thánh nào trả lời đc
Đúng 0
Bình luận (0)
À quên. I là giao của AB và MN. Mà ko cần trl đâu, t lm đc bài này r
Đúng 0
Bình luận (0)
cho (O,AB/2), E thuộc AB.Qua E vẽ dây CD vuông góc với AB. Trên BE lấy F vẽ các dây CM,DN đi qua F. chứng minh CMND cân
Cho đường tròn tâm O đường kính AB, M là điểm chính giữa của một nửa đường tròn (O) với đường kính AB, C là điểm bất kỳ trên nửa còn lại, CM cắt AB tại D. Vẽ dây cung AE vuông góc với CM tại F (E nằm trên đường tròn).Chứng minh rằng tứ giác ACEM là hình thang cân.Vẽ CH vuông góc với AB (H nằm trên đoạn AB). Chứng minh rằng CM là phân giác góc HCO.Chứng minh rằng CDlefrac{1}{2}AE.
Đọc tiếp
Cho đường tròn tâm O đường kính AB, M là điểm chính giữa của một nửa đường tròn (O) với đường kính AB, C là điểm bất kỳ trên nửa còn lại, CM cắt AB tại D. Vẽ dây cung AE vuông góc với CM tại F (E nằm trên đường tròn).
Chứng minh rằng tứ giác ACEM là hình thang cân.Vẽ CH vuông góc với AB (H nằm trên đoạn AB). Chứng minh rằng CM là phân giác góc HCO.Chứng minh rằng \(CD\le\frac{1}{2}AE\).1) Vì ^AEB chắn nửa đường tròn (O) nên EA vuông góc EB. Do đó BE // CM.
Suy ra tứ giác BECM là hình thang cân (Vì 4 điểm B,C,M,E cùng thuộc (O))
Kết hợp với M là điểm chính giữa cung AB suy ra CE = BM = AM hay (CE = (AM
Vậy thì tứ giác ACEM là hình thang cân (đpcm).
2) Đường tròn (O) có M là điểm chính giữa cung AB, suy ra MO vuông góc AB
Từ đó MO // CH suy ra ^HCM = ^OMC = ^OCM. Vậy CM là phân giác của ^HCO (đpcm).
3) Kẻ đường kính MG của đường tròn (O). Dễ thấy ^DOG = ^DCG (= 900)
Suy ra 4 điểm C,D,O,G cùng thuộc đường tròn đường kính DG
Mặt khác AB là trung trực của MG, D thuộc AB nên DG = DM
Theo mối quan hệ giữa đường kính và dây ta có:
\(CD\le DG=DM\Leftrightarrow2CD\le DM+CD=CM\Leftrightarrow CD\le\frac{1}{2}CM\)
Lại có tứ giác ACEM là hình thang cân, do vậy \(CD\le\frac{1}{2}CM=\frac{1}{2}AE\)(đpcm).
Dấu "=" xảy ra khi và chỉ khi C là điểm chính giữa cung AB không chứa M của (O).
Đúng 0
Bình luận (0)
Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE R
2
. Vẽ dây CF đi qua E. Tiếp tuyên của đường tròn tại F cắt CD tại M, vẽ dây Aỉ cắt CD tại N. Chứng minh:a, Tia CF là tia phân giác của góc BCDb, MF và AC song songc, MN, OD, OM là độ dài 3 cạnh của một tam giác vuông
Đọc tiếp
Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = R 2 . Vẽ dây CF đi qua E. Tiếp tuyên của đường tròn tại F cắt CD tại M, vẽ dây Aỉ cắt CD tại N. Chứng minh:
a, Tia CF là tia phân giác của góc BCD
b, MF và AC song song
c, MN, OD, OM là độ dài 3 cạnh của một tam giác vuông
a, Học sinh tự chứng minh
b, Chứng minh: A F M ^ = C A F ^ ( = A C F ^ ) => MF//AC
c, Chứng minh: M F N ^ = M N F ^ => ∆MNF cân tại M => MN = MF
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nên DOFM vuông => ĐPCM
Đúng 0
Bình luận (0)
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
Xét (O) có
\(\widehat{AEB}\) là góc nội tiếp chắn nửa đường tròn
nên \(\widehat{AEB}=90^0\)
Xét tứ giác BEFI có
\(\widehat{BEF}+\widehat{FIB}=180^0\)
nên BEFI là tứ giác nội tiếp
hay B,E,F,I cùng thuộc 1 đường tròn
Đúng 0
Bình luận (0)
Cho đường tròn (O;4cm), đường kính AB. Lấy điểm M trên đoạn OB sao cho BM=2cm, qua M vẽ dây CD của đường tròn (O) vuông góc với OB.
a) chứng minh tam giác ACB vuông và tính BC
b) chứng minh OCBD là hình thoi
c) trên tia đối của tia BA lấy điểm E sao cho BE=4cm. Chứng minh EC là tiếp tuyến của (O)
GIẢI GIÚP EM VỚI Ạ, EM ĐANG CẦN GẤP HUHU😢 EM CẢM ƠN NHÌU❤💏
Xem chi tiết
Cho đường tròn tâm O đường kính AB. Vẽ dây cung CD vuông góc với AB tại I ( I nằm giữa A và O ). Lấy điểm E trên cung nhỏ BC (E khác B và C) AE cắt CD tại F . Chứng minh: bốn điểm B E F I thuộc một đường tròn.
a) \(\Delta ABE\)nội tiếp đường tròn đường kính \(AB\)
\(\Rightarrow\)\(\Delta ABE\perp E\)
\(\Rightarrow\)\(AEB\lambda=90\)độ
Tứ giác\(BEFI\)nội tiếp đường tròn đường kính \(FB\)
cho đường tròn tâm O và 1 dây AB , vẽ đường kính CD vuông góc AB (D thuộc AnB^ trên cung nhỏ BC^ lấy điểm N . Các đường thẳng CN, DN cắt cạnh AB tại E, F . Trung tuyến của đường tròn tâm O tại N cắt cạnh AB tại I . Cm: IN=IF=IE

















